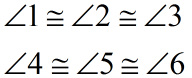|
 |
Use only your compass and straight edge when drawing a construction. No free-hand drawing! |
|
Divide a Segment into n Equal Parts (Partitions) |
|
We have seen how to bisect a segment into two equal parts. But what do we do if we need to divide a segment into more than just two equal parts? Well, we have a couple of choices.
Divide into 2, 4, 8, 16, ... equal parts (powers of 2: 21, 22, 23, 24, ...):
If the number of equal parts you need to create is a power of 2, you can simply start by bisecting the segment into 2 equal parts, and then continue bisecting the newly formed segments.
Given: 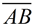 (a line segment) (a line segment)
Construct: divide 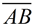 into 4 equal parts into 4 equal parts
STEPS:
1. Bisect 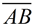 and label point C. and label point C.
2. Now, bisect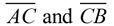 and label points D and E. and label points D and E.
You now have four equal divisions of 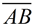 . .
|
 This construction only works if the number of divisions of equal parts is a power of 2, such as 2, 4, 8, 16, ...
This construction only works if the number of divisions of equal parts is a power of 2, such as 2, 4, 8, 16, ... |

Divide into n equal parts (where n is any integer value greater than 2):
Things get a bit trickier when the number of equal parts is not a power of 2. We will now be using a concept that pertains to parallel lines. We will be copying corresponding angles to create parallel lines (just as we did in our construction of parallel lines). Let's look at the construction first, and then we will see why it actually works.
Given: 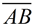 (a line segment) (a line segment)
Construct: divide 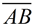 into 3 equal parts into 3 equal parts
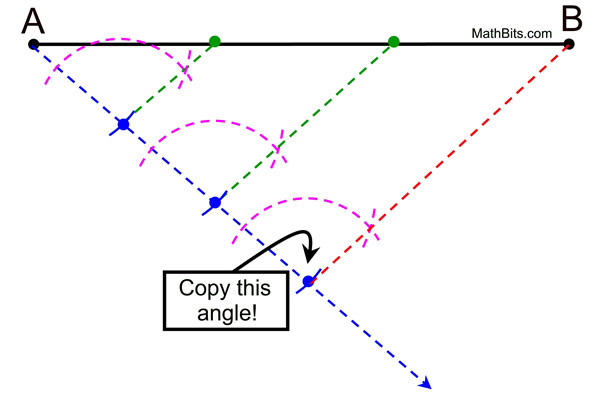
STEP 1: Draw a ray, starting at A and extending diagonally below the segment.
Set your compass to a comfortable span, place point on A and mark off an arc on the ray.
Move the point to where the arc crosses the ray and mark another arc on the ray.
Continue for three such arcs.
You will now have the three BLUE dots shown.
STEP 2: Connect the last blue dot to point B.
STEP 3: Copy the angle at the bottom of the newly formed triangle up at each of the other 2 blue dots. You will be copying corresponding angles to create parallel lines.
STEP 4: Draw the side of the copied angle sufficiently long as to intersect 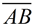 . You have now divided . You have now divided 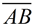 into three equal parts. into three equal parts.
This same construction process works for any number of equal divisions of three or more.
For example, if 5 equal divisions are needed, simply make 5 arcs on the ray in Step 1.
Then copy the bottom angle at each of the dots above it on the ray.
 Be very exact when doing this construction, as the slightest bauble Be very exact when doing this construction, as the slightest bauble
will throw off your divisions of the segment. |

This construction is based upon a theorem that states:
"If three or more parallel lines cut off congruent segments on one transversal,
they cut off congruent segments on all transversals."
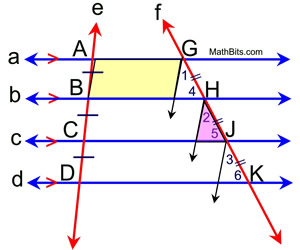
Given: a || b || c || d
Congruent segments on transversals as marked.
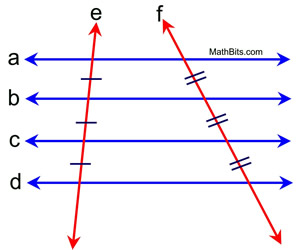
If congruent segments occur on transversal e, then they also will occur on transversal f.
|
If we show the transversals intersecting, you can see how the diagram more closely resembles our construction.
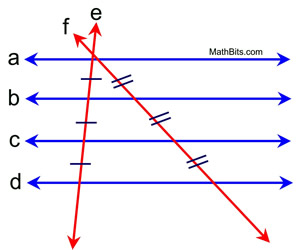
This diagram resembles our construction.
|

Here is a quick over-view of how this theorem can be proven.
Proof of Construction:
Start by drawing auxiliary lines through G, H, J and K that are parallel to transversal e, thus also parallel to each other. The Parallel Postulate justifies this step.
These parallel lines create a series of parallelograms whose right and left hand sides are congruent. Since 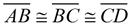 , we also have all three of the right hand sides of the parallelograms congruent to one another. , we also have all three of the right hand sides of the parallelograms congruent to one another.
Since parallel lines have corresponding angles congruent, we have
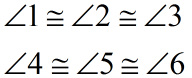
The small triangles with their top vertices at G, H and J are now congruent by Angle-Angle-Side.
|
Given: a || b || c || d
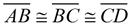
Prove: 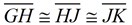
 |
By CPCTC, we have 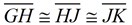 , thus proving our theorem to be true. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|