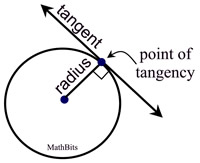
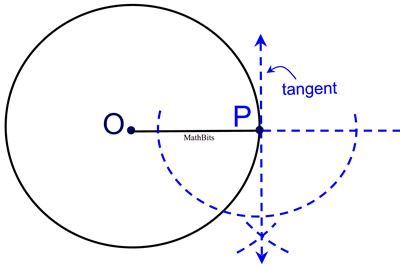
Proof of Construction: By construction, the line through point P is perpendicular to the line through O and P. The line through P is tangent to circle O, as verified by the theorem:
Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|