|
 |
Use only your compass and straight edge when drawing a construction. No free-hand drawing! |
|
 |
You already know all of the constructions that are used to prepare the constructions for SSS, SAS, and ASA. Just remember to draw the last two constructions in the needed order. |
|
Given: three segments
Construct: a triangle whose sides are these segments |
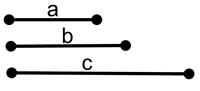 |
 You may run into a "trick" question where the given segments will NOT form a triangle. Remember that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. If this relationship does not occur, you will NOT be able to draw a triangle. You may run into a "trick" question where the given segments will NOT form a triangle. Remember that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. If this relationship does not occur, you will NOT be able to draw a triangle.
This SSS construction will be to "copy a segment" three times.
Steps:
1) Draw a reference line, if one is not given, and place a starting dot (A).
2) Copy segment c. With compass, measure the span of segment c. It is usually easier to start with the longest segment. (Place a small arc to show that you measured the segment.)
3) Place compass point on A and transfer this span with a small arc crossing the reference line. (Label B.)
4) Copy segment b. With compass, measure span of segment b.
5) Place compass point on A and transfer the span of b making an arc above the reference line.
6) Copy segment a. With compass, measure span of segment a.
7) Place compass point on B and transfer the span of a making an arc above the reference line, intersecting with previous arc. (Label C.)
8) Connect points A, B and C for ΔABC.
|
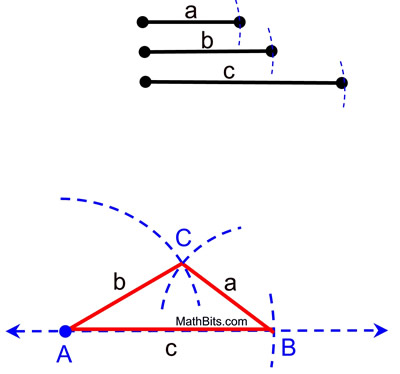
Notice the labeling in this construction. It is customary to label vertices with capital letters and segments with single small case letters. Also notice that the small case a is placed opposite vertex A, and so on.
|
 All triangles constructed with these three segments will be congruent. All triangles constructed with these three segments will be congruent.

Given: two segments and one angle
Construct: a triangle such that the angle will be included between the two given segments (sides) |
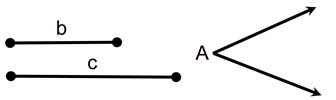 |
The SAS order of the construction will be "copy a segment", followed by "copy an angle", followed by "copy a segment" again.
Steps:
1) Draw a reference line, if one is not given, and place a starting dot (A). We will be copying our angle's vertex at this point.
2) Copy segment c. With compass, measure the span of segment c.
3) Place compass point on A and transfer this span with a small arc crossing the reference line. (Label B.)
4) Copy angle A. Place compass at vertex of the given angle. Swing an arc crossing both sides of the angle. Keep this compass span.
5) Without changing compass span, place compass point at A on the reference line and draw this arc sufficiently large and crossing the reference line.
6) Return to the given angle and measure span across the arc with the compass.
7) Without changing compass span, transfer this span to your arc on the reference line, and draw a ray from A through the point of intersection.
8) Copy segment b. With compass, measure the span of segment b and mark it off on the new ray created in your construction. (Label C.) Draw ΔABC.
|
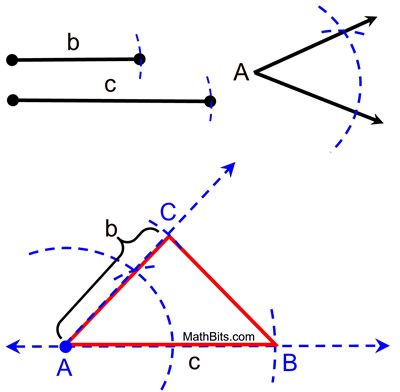
It is helpful to remember this
construction in the SAS order:
copy side
copy angle
copy side
|
 |
All triangles constructed with these sides and this angle, in this ordered pattern, will be congruent. |

Given: two angles and one side
Construct: a triangle such that the side will be included between the two given angles |
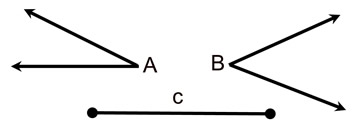 |
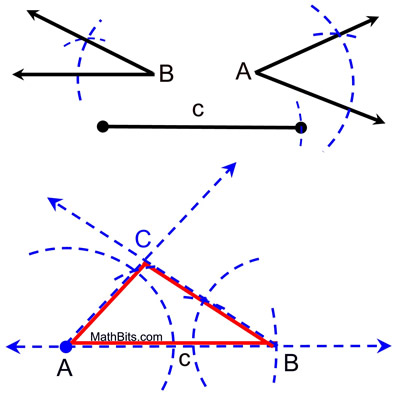
The ASA order of the construction will be "copy an angle", followed by "copy a segment", followed by followed by "copy an angle" again.
Steps:
1) Draw a reference line, if one is not given, and place a starting dot (A). We will be copying our angle A's vertex at this point.
2) Copy angle A. Place compass at vertex of the given angle A. Swing an arc crossing both sides of the angle. Keep this compass span.
3) Without changing compass span, place compass point at A on the reference line and draw this arc sufficiently large and crossing the reference line.
4) Return to given angle A and measure span across the arc with the compass.
5) Without changing compass span, transfer this span to your arc on the reference line, and draw a ray connecting A to the point of intersection.
6) Copy segment c. With compass, measure the span of segment c.
3) Place compass point on A and transfer this span with a small arc crossing the reference line. (Label B.)
8) Copy angle B. Repeat directions above for copying angle B at point B.
9) Label the point of intersection of the two angle rays as C. Draw ΔABC.
|
It is helpful to remember this
construction in the
ASA order:
copy angle
copy side
copy angle
|
 |
All triangles constructed with these angles and this side, in this ordered pattern, will be congruent. |


NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|







