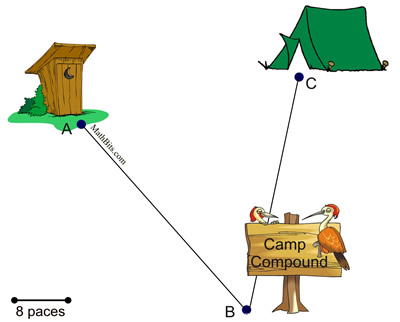
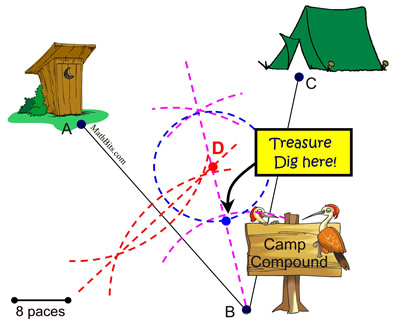
A compound locus problem utilizes the basic locus theorems that you already know.
Good news -- there are no new theorems!
Solving Compound Locus Problems: When two locus conditions appear in a problem, you need to prepare each condition separately on the same diagram. After drawing the two separate conditions, the solution will be the locations where the two loci intersect. Let's review the strategies for solving locus problems, with an emphasis on compound locus. 1. Draw a diagram using the given information. 2. Read carefully to determine what conditions need to be satisfied. Look for the words "AND" or "AND ALSO" separating the conditions, and choose the first locus condition. 3. Plot the first locus condition only. If you do not immediately see the first condition as an application of an existing locus theorem, start by finding ONE point that satisfies the needed conditions and plot it on your diagram. Then find several additional points that satisfy the conditions and plot them as well. Continue plotting points until you can see the pattern, or path, that is developing, and you see which locus theorem is needed. 4. Draw a dashed line, or circle, through the plotted points to show the first locus. 5. Now, plot the second locus condition on the same diagram. Temporarily ignore the first condition. Follow steps 3 and 4 again to prepare this second condition. 6. The location where the dashed lines (or circles) intersect will be the points which satisfy both conditions. These points of intersection will be your answer to the compound locus problem.
Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
||||||||||||||||