Practice Page
Directions: Read each question carefully. Choose the best answer.
1.
The diagram at the right shows the construction of line a, through point P, parallel to line b.

Which theorem was used to justify this construction?
Choose:
basicpracc1
 
If two lines are perpendicular to the same line, the lines are parallel.
If two lines are cut by a transversal and the interior angles on the same side of the transversal are supplementary, the lines are parallel.
If two lines are cut by a transversal and the corresponding angles are congruent, the lines are parallel.
If two lines are cut by a transversal and the alternate interior angles are congruent, the lines are parallel.

 

 

2.
Which diagram shows the correct construction for an angle bisector?
 
Choose:

basic2b

basic2a

basic2c
basic2d

 

 

3.
Kyle is attempting to bisect the obtuse angle shown at the right. He does not understand why his arcs in the interior of the angle are not intersecting one another. What has Kyle done incorrectly?
Choose:
basic3
 
Kyle placed his compass point in the wrong place to draw the interior arcs.
Kyle's interior arcs will intersect if he draws more of the arcs.
Kyle did not stretch his compass sufficiently wide to create the interior arcs.
Kyle drew the first arc incorrectly.

 

 

4.
Which of the following statements is a result of the construction shown at the right?
Choose:
basic4b
basic4a
D is the midpoint of AB2
All three choices are true.
basicprac4

 

 

5.
Based on the construction shown at the right, which of the following statements must be true?

Choose:
basic55
basic54
basic51
basic53

basic5

 

 

6.
Which diagram shows the correct construction for a perpendicular bisector of the segment from P to R ?
 
Choose:

basic61

basic62

basic63
basic6

 

 

7.
Based on the construction shown at the right, which of the following statements must be true?

Choose:
m∠1 = m∠2
m∠3 = m∠4
m∠3 = m∠2
m∠1 = m∠3

basic7

 

 

8.
Which of the following choices was the FIRST step in drawing this construction of an angle bisector?

Choose:
From points R and T, draw arcs with equal radii intersecting at Q.
From point S, draw an arc intersecting the sides (rays) of the angle (and label the points R and T).
Draw the ray connecting S to Q.
Measure the span of the arc from R to T.

basic8

 

 

9.
When the construction "Copy an Angle" is finished, segments are drawn across the span of the arcs (as shown below in red). Which method proves the two triangles formed are congruent?

Choose:
ASA
SAS
SSS
AAS
 
basic9

 

 

10.
When constructing the bisector of a line segment, you are also constructing the perpendicular bisector of the segment.

Choose:
TRUE
FALSE
basic10

 

 

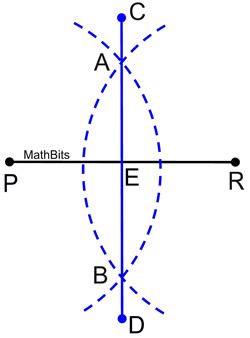
11.
Regarding the construction shown at the right, which statement is NOT always true?

Choose:
basic11a
ER = ½ PR
basic11b
m∠AER = 90º
basic11

 

 

12.
When constructing a line, through a point, parallel to a given line, you will be

Choose:
copying an angle.
copying a segment.
bisecting a segment.
constructing a perpendicular.
basicredheadboy

 

 

13.
Alison is attempting to construct a perpendicular to line m at point P. She placed her compass point at P and drew the arc intersecting the line at two points she labeled A and B.
basic13err
 
She then placed her compass at point A and made an arc, and at point B and made an arc. Unfortunately, her arcs are tangent to one another at point P. She does not have two points to connect to form the perpendicular. What did she do wrong?

Choose:
 
Alison needed to place her compass point at P to draw two intersecting arcs.
Alison needed to make one of the arcs larger so they will intersect.
Alison needed to increase the span on her compass after drawing the first arc.
Alison is not wrong - she just needed to eyeball the line through point P.

 

 

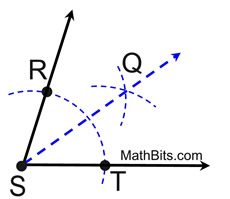
14.
The construction of an angle bisector is verified by the creation of two congruent triangles. In the construction at the right, the congruent triangles will be ΔSRQ and ΔSTQ. Which theorem proving triangles congruent is used for these two triangles?

Choose:
SAS
ASA
AAS
SSS

basic8

 

 

15.
The task of constructing a perpendicular to a given line at a point on the line is based upon which other construction?

Choose:
the bisector of a segment
a perpendicular from a point off the line
the copy of a segment
the copy of an angle
basicperpgirl

 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".