|
There are certain problems that are difficult to prove "directly" (starting with the GIVEN and working toward the PROVE). In these problems, it may be helpful to ask yourself,
"What will happen if the statement I am trying to prove is NOT true?"
This reasoning is the premise of the Indirect Proof, or Proof by Contradiction.
Indirect Proof:
Assume what you need to prove to be FALSE, and then show that something contradictory (or absurd) will happen. |
Proof by Contradiction
is known, in Latin, as
"reductio ad absurdum"
meaning
"reduced to an absurdity".
|
|
|
How to Recognize When an Indirect Proof May be Needed:
In most cases, the word NOT, or the "not" symbol (such as ≠ ) will appear in a problem requiring an Indirect Proof.
|
|
Steps in an Indirect Proof:
• |
Look for the word NOT or a "not" symbol in the problem |
• |
Assume the opposite of what you are trying to PROVE is true. |
• |
Proceed with the proof as you would in a normal direct proof. Use valid statements and reasons. |
• |
Search for a conclusion that will contradict given or known geometric information in this problem. In most cases, you will find something that contradicts a piece of GIVEN information. |
• |
When you find this contradiction, you will know that your assumption is false. |
• |
If the assumption (the opposite of the PROVE) is false, then the original PROVE statement in this problem must be true. Your job is done! |

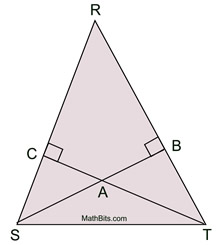
Example:
|
STATEMENTS |
REASONS |
1. |
Assume 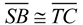 Assume the opposite of the Prove.
Assume the opposite of the Prove. |
1. |
Assumption leading to a contradiction. |
2. |
|
2. |
Given |
3. |
|
3. |
An altitude of a triangle is a segment from any vertex perpendicular to the line containing the opposite side. |
4. |
∠TCR and ∠SBR are right angles |
4. |
Perpendicular lines meet to form right angles. |
5. |
∠TCR  ∠SBR ∠SBR |
5. |
All right angles are congruent. |
6. |
∠R  ∠R ∠R |
6. |
Reflexive property |
7. |
|
7. |
AAS - if 2 ∠s and the non-included side of one Δ are  to the corresponding parts of another Δ, the Δs are  . |
8. |
|
8. |
CPCTC - corresponding parts of congruent triangles are congruent. |
9. |
ΔSRT is isosceles
This contradicts the GIVEN that the triangle is scalene (meaning no congruent sides). |
9. |
An isosceles triangle has 2 congruent sides. |
10. |
|
10. |
Contradiction steps 9 and 2. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|