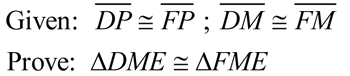One of the beauties of proving triangles congruent is that you have left-over pieces that you also know are congruent. These left-over corresponding pieces are often the information you are asked to prove, using CPCTC ("Corresponding parts of congruent triangles are congruent.").
Now that you feel more secure with congruent triangle proofs, it is time to look at more challenging problems where left-over parts from one set of congruent triangles are used to prove another set of triangles congruent. Thus, the title "double congruency" where there will be two sets of congruent triangles in one problem.
| Double Congruency - Using Two Sets of Congruent Triangles: |
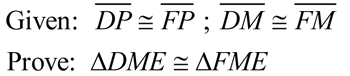
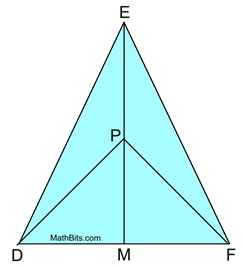
Let's start by examining what we have to use, and what additional information we may need, to solve this problem. The only information we have that pertains to the triangles we are to prove congruent, are the sides 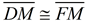 and the fact that the triangles share a side from M to F. We are missing one additional piece of information. We do NOT know that this is a large isosceles triangle and we do not know that there are right angles at M.
and the fact that the triangles share a side from M to F. We are missing one additional piece of information. We do NOT know that this is a large isosceles triangle and we do not know that there are right angles at M.
While we seem to be missing information in our desired triangles, there are two other triangles that we can show to be congruent, and their left-over pieces will give us the additional information we need. Let's see how this will work.
STATEMENTS |
REASONS |
1. |
|
1. |
Given |
2. |
|
2. |
Reflexive Property |
3. |
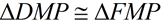 We are proving this set of triangles congruent to obtain additional information to use in proving our needed triangles congruent.
We are proving this set of triangles congruent to obtain additional information to use in proving our needed triangles congruent. |
3. |
SSS - If 3 sides of one triangle are congruent to the corresponding sides of another triangle, the triangles are congruent. |
4. |
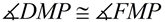 These angles can be used as parts of the triangles we need to prove congruent.
These angles can be used as parts of the triangles we need to prove congruent. |
4. |
CPCTC - corresponding parts of congruent triangles are congruent. |
5. |
|
5. |
Reflexive Property |
6. |
|
6. |
SAS - If 2 sides and the included ∠ of one triangle are congruent to the corresponding sides of another triangle, the triangles are congruent. |