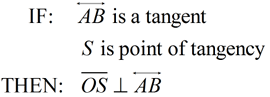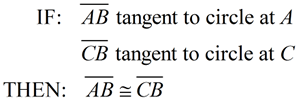|
A tangent line to a circle plays an important role in our investigation of circles,
even though it never enters the interior of the circle.
|
A tangent to a circle is a line in the plane of the circle that intersects the circle in exactly one point. |
|
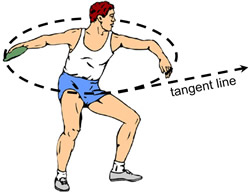 |
The discus throw is a track and field event in which an athlete attempts to throw a heavy disc (called a discus) further than his or her competitors. The athlete spins counterclockwise around one and a half times through a circle, then releases the throw. When released, the discus travels on a path that is tangent to the circular spin orbit. |
Common tangents are lines, rays or segments that are tangent
to more than one circle at the same time.
4 Common Tangents
(2 completely separate circles)
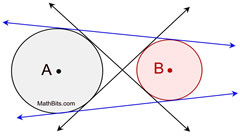 2 external tangents (blue)
2 external tangents (blue)
2 internal tangents (black)
|
3 Common Tangents
(2 externally tangent circles)
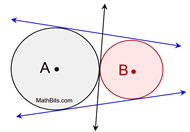 2 external tangents (blue)
2 external tangents (blue)
1 internal tangent (black)
|
2 Common Tangents
(2 overlapping circles)
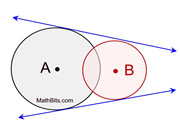 2 external tangents (blue)
2 external tangents (blue)
0 internal tangents
|
1 Common Tangent
(2 internally tangent circles)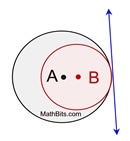
1 external tangent (blue)
0 internal tangents
|
0 Common Tangents
(2 concentric circles)
Concentric circles are circles
with the same center.
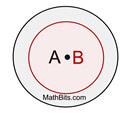 0 external tangents
0 external tangents
0 internal tangents
|
(one circle floating inside
the other, without touching)
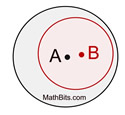 0 external tangents
0 external tangents
0 internal tangents
|
|

|
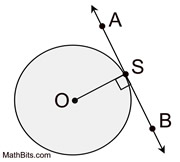
If a line is tangent to a circle, it is perpendicular to the radius drawn to the point of tangency. |
 |
|
|
|
Example:

Given a tangent with a radius
drawn to the point of tangency.
Find x.
|
Solution:
• In this diagram, the radius is perpendicular to the tangent at the point of tangency, forming the right triangle shown.
Since OB = 6, the missing portion to complete OA is also 6 (a radius length), making OA = 10.
Using Pythagorean Theorem, x = 8.
c2 = a2 + b2
102 = 62 + x2
|
|
PROOF:
Remember, we proved, when working with perpendiculars, that "the shortest distance from a point to a line is the perpendicular distance". In this new proof, we will determine whether it is possible for the perpendicular distance to NOT be the shortest distance.


We know, by the definition of a tangent to a circle, that the tangent line intersects the circle at only ONE point.
That point is S.
When we draw a new segment from O to the tangent, its length will have to stretch beyond the outside edge of the circle.
(length OPD with radius OP)
|
This situation requires an indirect proof (a proof where you assume something to be true and then prove that this assumption leads to a contradiction of a known fact).

|
|

|
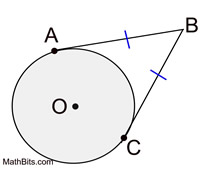
Tangent segments to a circle from the same external point are congruent.
(You may see this theorem referred to as the "hat" theorem as the circle appears to be wearing a hat.) |
| |
|
|
|
Example:
|
Solution:
• In this diagram, AB = AC.
2x + 15 = 45
2x = 30
x = 15
|
|
PROOF:
With the help of the previous theorem, this theorem can be easily proven. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|