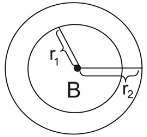
Figures can be proven similar if one, or more, similarity transformations (reflections, translations, rotations, dilations) can be found that map one figure onto another. In our attempt to prove all circles are similar, a translation and a scale factor (from a dilation)
will be found to map one circle onto another.
A circle, by definition, is the set of points equidistant from a given point.
Consequently, a circle is defined by only one length - the radius.
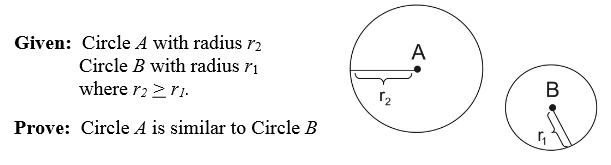
Proof:
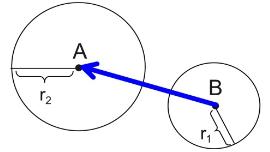
• Move the center of the smaller circle onto the center of the larger circle. Translate circle B, by vector 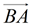 , onto circle A. The circles are now concentric (they have the same center).
• A dilation is needed to increase the size of circle B to coincide with circle A.
A value that when multiplied by r1 will create r2 is needed.
The scale factor, x, to increase circle B:
 |
|
• A translation, followed by a dilation with scale factor 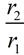 will map one circle onto the other, thus proving that the circles are similar. • We found the similarity transformations! |