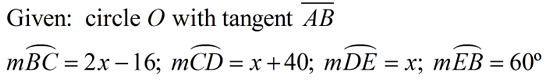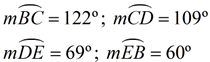Find the measures of the arcs:
2 x - 16 + x + 40 + x + 60 = 360
4 x + 84 = 360
x = 69
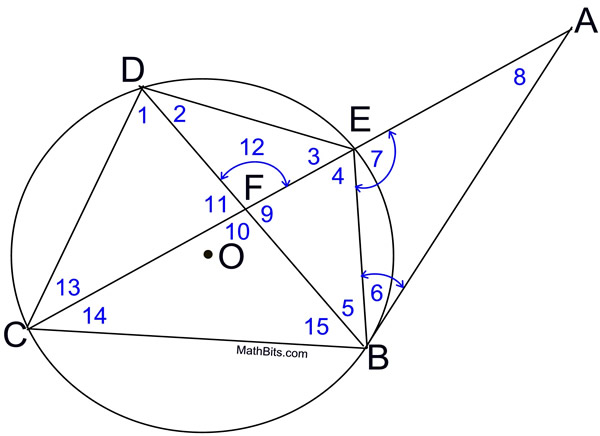
 Label the diagram with the arcs.
Label the diagram with the arcs. |
∠1 is an inscribed angle
m∠1 = ½ arc
=
½ (122)
m∠1= 61º |
∠2 is an inscribed angle
m∠2 = ½ arc
=
½ (60)
m∠2= 30º |
∠3 is an inscribed angle
m∠3 = ½ arc
=
½ (109)
m∠3= 54.5º |
∠4 is an inscribed angle
m∠4 = ½ arc
=
½ (122)
m∠4= 61º |
∠5 is an inscribed angle
m∠5 = ½ arc
=
½ (69)
m∠4= 34.5º |
∠6 is formed by a tangent and a chord
m∠6 = ½ arc
=
½ (60)
m∠6= 30º |
∠7 is "tricky"!!!
No ∠ formula works!
∠7 & ∠4 linear pair
m∠7 + m∠4 = 180º
m∠7 + 61º = 180
m∠7 = 119º
|
∠8 is formed outside by tangent and secant
m∠8 = ½ difference of arcs
=
½ (122 - 60)
m∠8= 31º |
∠s 9, 10, 11, 12 formed by 2 intersecting chords
m∠9 = ½ sum of arcs
=
½ (109 + 60)
m∠9 = 84.5º
m∠10 = 95.5 (linear pair)
m∠11 = 84.5º (vertical ∠)
m∠12 = 95.5º (vertical ∠) |
∠13 an inscribed angle
m∠13 = ½ arc
=
½ (69)
m∠13= 34.5º |
∠14 is an inscribed angle
m∠14 = ½ arc
=
½ (60)
m∠14= 30º |
∠15 is an inscribed angle
m∠15 = ½ arc
=
½ (109)
m∠15= 54.5º |
As with all math problems, there are also other ways to arrive at these answers. |