|
The theoretical aspect of geometry is composed of definitions and theorems. Definitions are precise descriptions of words used in geometry. Theorems are logical results deduced about these geometric definitions.
On this page, we will discuss precise definitions.
The word "precise"means exact and accurate.
 What do we know about definitions? What do we know about definitions? |
 |
A definition is the formal statement of the meaning or significance of a word. |
|
When working with definitions (and theorems), you will encounter the word "converse".
Converse is a logic term indicating the reverse of a statement written in "if-then" form.
(The concepts within the "if" and "then" portions of the statement switch places.)
Statement: If today is Tuesday, then it is laundry day.
Converse: If it is laundry day, then today is Tuesday.
Definitions are actually "bi-directional".
If you put a definition into "if - then" form, the definition will be remain true when the portions of the "if" and "then" statements are exchanged. Both the definition and its converse are true. Logically speaking, this is referred to as an "if and only if" situation, or a biconditional.
Example: Definition: A right triangle is a triangle with one right angle.
If-then form: If a triangle is a right triangle, then it is a triangle with one right angle. (true)
Converse (Reversed form): If a triangle has one right angle, then it is a right triangle. (true)
Biconditional: A triangle is a right triangle if and only if the triangle has one right angle. (true)
|
 What is a "precise" mathematical definition? What is a "precise" mathematical definition? |
A good mathematical definition explains "precisely" what something means. You may express definitions in your own words, as long as your definitions are "precise".
|
While expressing definitions in your own words sounds like a simple process, it can easily lead to faulty definitions and loss of credit on test papers. Be careful! |
Take a look at what problems arise when precision is lacking.
| Student's Definition: |
Counter-example to disprove student's definition: |
"Precise" Definition: |
Complementary angles
are angles adding to 90 degrees.
(Note: This definition is considered incorrect.) |
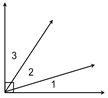 |
By the student's definition, ∠1, ∠2 and ∠3 could be complementary. |
This is not correct! |
Complementary angles
are TWO angles the sum of whose measures is 90.
|
If you choose to define terms "in your own words", be sure to express a degree of precision that will guarantee your definition is accurate.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

