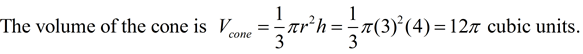|
In this section, we will be rotating (spinning) a two-dimensional figure about a line to produce a three-dimensional shape, called a solid of revolution.
|
A solid of revolution is a three-dimensional figure obtained by rotating a two-dimensional figure (or curve) around a straight line (called the axis) that lies in the same plane. |
|
An example of a rotation about a line is the concept of a revolving door. The panel of one section of the glass door is "pushed" about a center pole, creating an outer cylindrical path around the pole. While the revolving door does not create a "solid", it does illustrate the process of revolution. If the door filled the entire space as it revolved, a cylindrical solid would be formed.
With the idea of revolution (rotation) in mind,
let's start revolving some geometric shapes to create geometric solids.
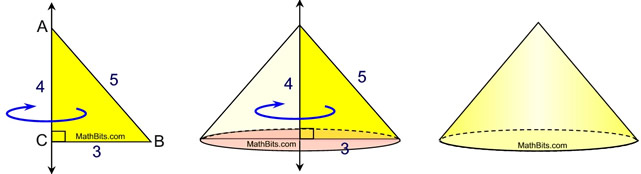
• Let's start by rotating right triangle ACB about a vertical line, as shown below. As the triangle is revolved about the line, the vertices A and C remain stationary, while vertex B follows the path of a circle. As the triangle rotates,  creates the outline of a cone. Since the triangle's interior is shaded, it creates the interior of the cone, creating a solid figure. |
|
|
Note: If the 2-D figure (or a portion of the figure) is shaded, then that portion of the 3-D figure will be solid when the revolution occurs. |
• In this problem, two semicircles are rotated about a vertical line. By the shading, we know that only the portion between the semicircles will create the 3-D solid. The cross-section of the solid shows that it resembles a round gum ball with a hollow center (a solid sphere with an empty sphere in its center). |
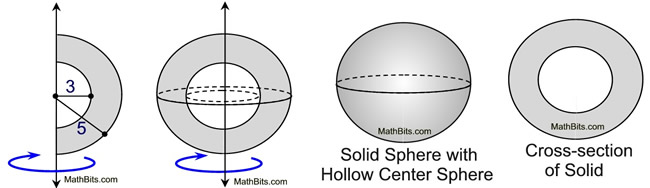
|
|
Note: If the 2-D figure is not tangent (touching) to the line of rotation (axes), then the solid will be in the form of a "ring", with an open section between portions of the solid. |
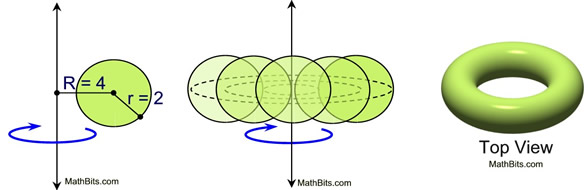
• This 2-D figure does not touch the line around which it is to be revolved. As a result, the 3-D solid will have a "ring" appearance (with an open center section). |
| |
This particular solid is called a torus, and looks like a dough-nut.
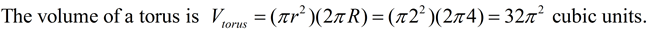 |
Note: The 2-D figure may appear on coordinate axes, from which you can obtain measurement information about the figure. Rotations will most likely be about the y-axis or the x-axis (but may be about any vertical or horizontal line.)
(Rotations about slanted lines in the coordinate plane will not be discussed at this level.) |
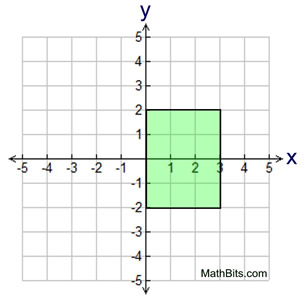
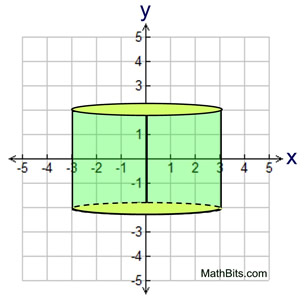
• A rectangle, shown in the coordinate plane (below, left), is to be rotated about the y-axis. Sketch the resulting solid on the grid and find its volume in cubic units.
The 3-D sketch, which is a cylinder, is shown below on the right. |
|
|
Using the coordinate grid, the width of the rectangle is 3 units and its height is 4 units. 
|
Note: It may be the case that a portion of a function (or functions) will represent the 2-D figure on coordinate axes to be revolved about an axis or a vertical or horizontal line.
(Rotations about slanted lines in the coordinate plane will not be discussed at this level.) |
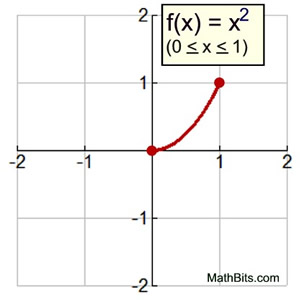
• The function f (x) = x2, on the domain 0 < x < 1, is graphed. The resulting graph is then revolved about the y-axis. Sketch the 3-D solid.
Will the volume of this solid be greater than or less than a cone of radius 1 unit and a height of 1 unit?
|
|
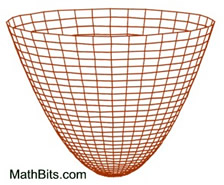
The volume of this shape will be slightly greater than the volume of a cone with comparable dimensions. This figure is broader near the vertex than a straight sided cone.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|