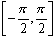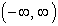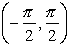|
Inverse Notation:
arcsin(x) = sin-1(x)
arccos(x) = cos-1(x)
arctan(x) = tan-1(x)
|

As stated at the left, the exponent of -1 denotes "inverse".
It does not mean 1/sin x, such as x-1 = 1/x.
|
 |
y = arcsin(x) = sin-1(x) solves the equation x = sin(y).
Read: arcsin(x) as "the angle whose sine is x". |
|
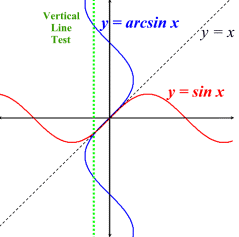
When working with the inverse of a function, we learned that the inverse of a function can be formed by reflecting the graph over the identity line y = x. We also learned that the inverse of a function may not necessarily be another function.
Look at the sine function (in red) at the right. If we reflect this function over the identity line, y = x, we will create the inverse graph (in blue). Unfortunately, this newly formed inverse graph is not a function. Notice how the green vertical line intersects the new inverse graph in more than one location, telling us it is not a function. (Vertical Line Test). |
|
By limiting the range to see all of the y-values without repetition, we can define inverse functions of the trigonometric functions. It is possible to form inverse functions at many different locations along the graph. The functions shown here are what are referred to as the "principal" functions.
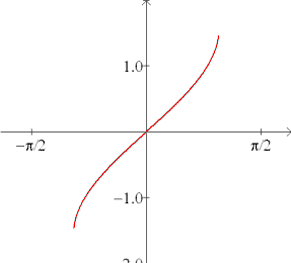
Inverse sine:
f (x) = sin-1(x)
f (x) = arcsin(x) |
Domain: [-1,1]
Range: 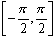 |
|
 |
| |
|
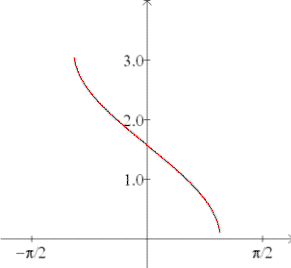
Inverse cosine:
| f (x) = cos-1(x)
f (x) = arccos(x) |
Domain: [-1,1]
Range: [0,π] |
|
 |
| |
|
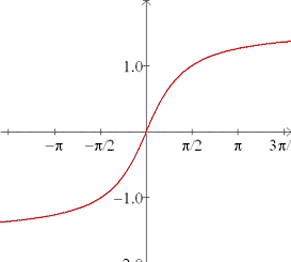
Inverse tangent:
| f (x) = tan-1(x)
f (x) = arctan(x) |
Domain: 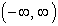
Range: 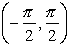 |
|
 |

|
For help with trigonometric inverses on
your calculator,
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|