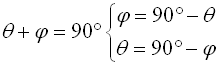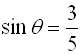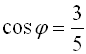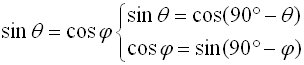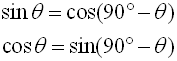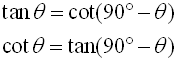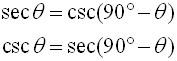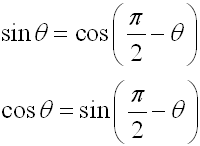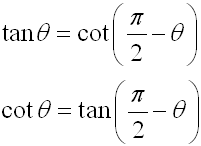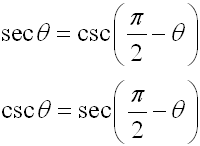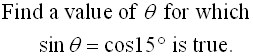The relationship between sine and cosine was examined in previous courses. That same type of relationship exists between other trigonometric functions as well. Let's take a look!
Such examinations, lead us to three sets of "cofunction" identities
Also written (in terms of radians):
Examples:
Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|

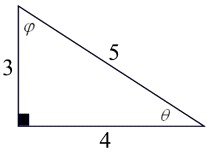
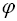 and
and 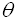 add to 90º. These angles are complementary angles.
add to 90º. These angles are complementary angles.