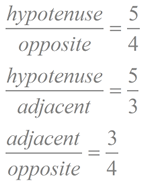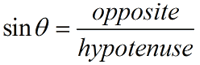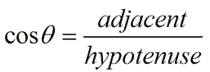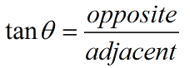A literal translation of "trigonometry" is "triangle measure". A trigonometric function relates one acute angle (non-right angle) of a right triangle to the ratio of the lengths of any two sides of the triangle. As we saw in Geometry with the 30º-60º90º and 45º-45º-90º triangles, once one angle in a right triangle is known, all right triangles with that same acute angle will be similar by Angle-Angle (AA). Such consistency allows for the creation of ratios regarding the lengths of the sides of such triangles.
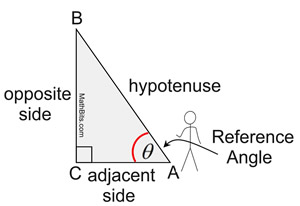
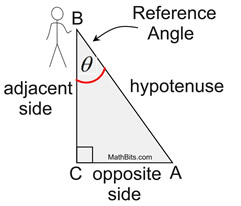
Trigonometric functions can operate with either of the two acute angles of a right triangle. A certain labeling is used to refer to the components of these triangles. This labeling is based upon which of the two acute angles is being used in the problem. Before you can use a trigonometric function, you need to have a "point of reference" from which to work, which is called your Reference Angle. Think of yourself as standing at the Reference Angle (the angle used in your problem). You know where the hypotenuse is located. The leg across from you is called the "opposite side", and the left-over leg is called the "adjacent side" (the leg "next" to you).
It is customary (but not mandatory) to use the Greek letter "theta" (θ)
as a label for a reference angle.
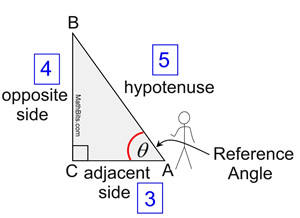
So, how many ratios pertaining to the sides of the triangle are possible? Let's take a look:
The ratios that we established above have specific "names". The first three ratios we created are called sine, cosine and tangent and are referred to as trigonometric functions.
We will be abbreviating the statements above to state: See how to solve for a missing side or a missing angle using trigonometry.
Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|