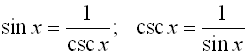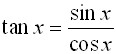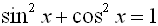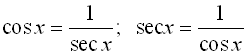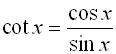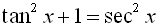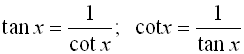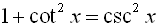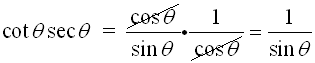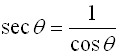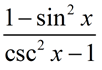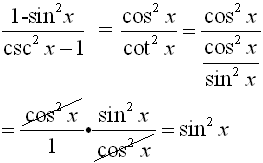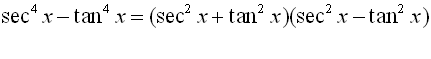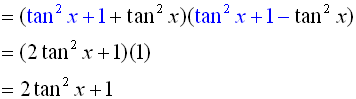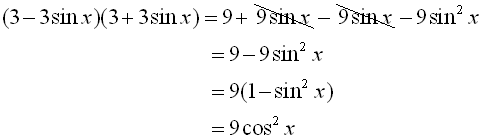We have seen the usefulness of the Pythagorean Trigonometric Identities. If we combine those identities with other trigonometric identities, we have a powerful set of tools to help simplify expressions, factor expressions, and solve equations involving trigonometric functions.
We know that in mathematics, being able to look at equivalent "forms"
of an expression or equation often sheds light on how to solve a problem. This toolbox of identities will help us look at problems from a different (but equivalent) viewpoint to reach a solution.
Trigonometric Identities Toolkit
 |
Suggestions to Keep in Mind:
•
When simplifying expressions, or factoring expressions,
look for common factors.
• If none exist, look for related functions from the identities
that will assist in the simplification.
|
 |
Simplify: cot θ sec θ in terms of sin θ |
| |
Solution:
The objective is to replace cot and sec with expressions that contain sin, so as to introduce sin into the expression.
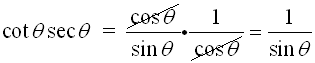
|
Substitutions from toolkit:
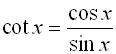
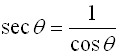
|
|

 |
Simplify: 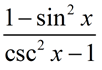 |
| |
Solution:
Look carefully! The numerator and the denominator are "versions" of the Pythagorean Identities.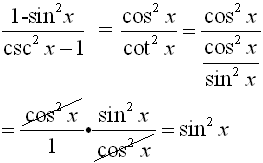
|
Pythagorean Identities:
1 - sin2x = cos2x
csc2x - 1 = cot2x
Substitute:
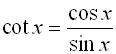
|
|