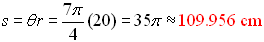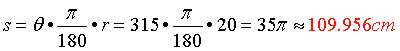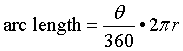|
(The arc length discussed on this
page will be in relation to a circle.) |
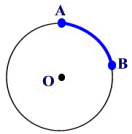
An arc of a circle is a "portion" of the circumference of the circle.
The length of an arc is simply the length of its "portion" of the circumference. Actually, the circumference itself can be considered an arc length.
|
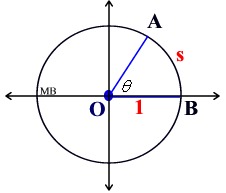
The length of an arc (or arc length) is traditionally symbolized by s.
In the diagram at the right, it can be said that "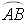 subtends angle θ ". subtends angle θ ".
| Definition: subtend - to be opposite to |
|
|

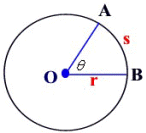
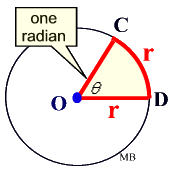
If the length of an arc of a circle, s, (think of straightening it out), is the same as the length of the circle's radius, r, a specific situation occurs. The angle, θ, created by this situation is called a radian.
|
A radian is the measure of an angle θ that, when drawn as a central angle, subtends an arc whose length equals the length of the radius of the circle.
The measure of θ ( or m<COD ) = 1 radian
|
|
|
When radius r = arc length r, the angle θ measures 1 radian.
(Thus the naming of "radian" with its connection to "radius".)
Radian measure is another way of expressing the measure (size) of an angle.
It is considered to be a "pure" measure since it is based upon the radius
of the circle being wrapped along the circumference.
While at first it may seem easier to work with degrees, you will find that there is a mathematical simplicity to the use of radians.
So, now we have two methods of expressing the measure of an angle: in degrees and in radians.
When comparing radians to degrees, one radian is approximately 57.2958... degrees.

A radian is
represented
by the
symbol rad.
|
The radian measure of a central angle θ of a circle is defined as the ratio of the length of the arc the angle subtends, s, divided by the radius of the circle, r.
|
|

Relationship between Degrees and Radians: |
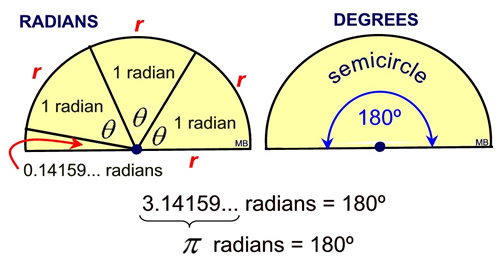
Take a look at the two semicircles at the right.
If we "wrap" the radius, r, along the circumference of a semicircle (first diagram), we will need 3 radii plus a "bit more" to complete the semicircle. The number of radians needed to represent the central angle of a semicircle is approximately 3.14159 radians. Yes, that is π !
|
|
We know that the central angle in a semicircle contains 180º. So we have π radians equivalent to 180º, and we now know:
• π radians = 180º
• 1 radian ≈ 57.29577951º (divide by π).
• 2π radians = 360º |
|
 |
|
|
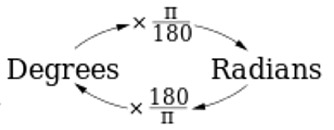
To change
from degrees to radians,
multiply by 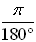 |
|
To change
from radians to degrees,
multiply by 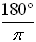 |
|
|
Hint for remembering the relationship
between radians and degrees:
|
|
Solve for D (degres) or
R (radians) to get the proper conversion formula. |
|

 Convert 50º to radians. Answer: Convert 50º to radians. Answer: 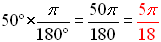 |
 Convert Convert 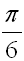 to degrees. Answer: to degrees. Answer: 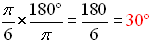 |
Note: if the size of an angle is stated as a value without the degree symbol, then the angle is assumed to be in radian measure.

When dealing with arc length, this same strategy of converting between degrees and radians can be used when given the angle, θ, in degrees.
θ in RADIANS
Arc length of a circle:
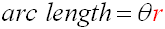
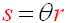
|
|
θ in DEGREES
Arc length of a circle:
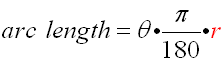 |
|
 |
When the arc length equals an entire circumference (2πr), we can use s = θ • r to get
2πr = θ • r and 2π = θ. This verifies what we already know to be true, that 2π = 360º. |
 |
Remember that the formula for arc length (with the angle in degrees) is often expressed using the angle to create a fractional part of the entire circle (360º), multiplied by the total circumference of the circle.
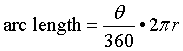 If simplified, this formula is the same formula shown above.
If simplified, this formula is the same formula shown above.
|

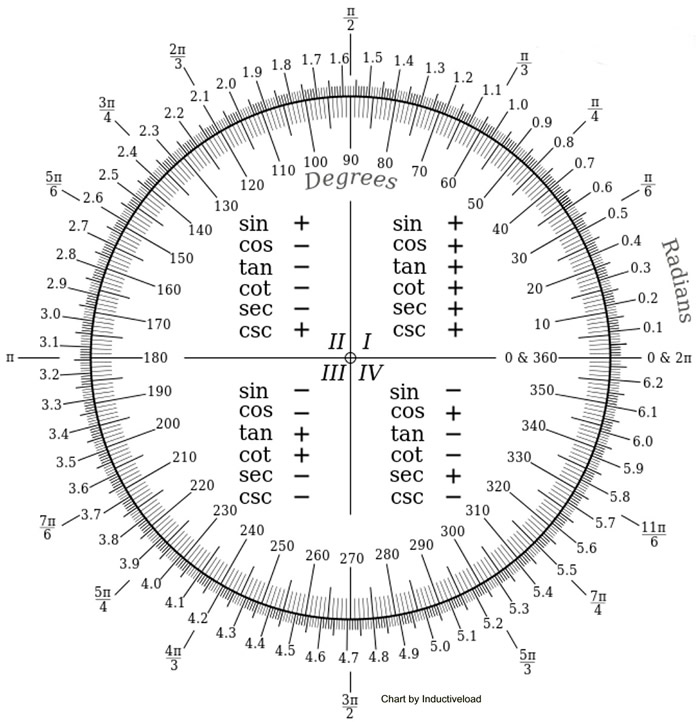
The following chart will give you a feel for the relationship between degrees and radians. It reads as a unit circle, starting at the right, 0º, and moving counterclockwise around the circle. Degrees are on the inner rim of the circle. Radians, expressed to nearest tenth and in terms of π, are on the outer rim of the circle.
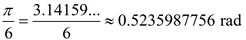

|
For help with radians and degrees on
your calculator,
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|


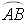 subtends angle θ ".
subtends angle θ ".
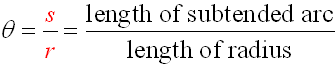
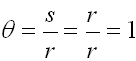
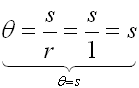

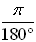
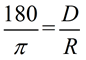
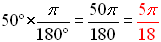
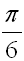 to degrees.
to degrees.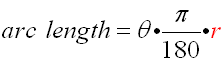

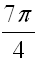 radians on a circle of radius 20 cm?
radians on a circle of radius 20 cm?