|
Directions: Utilize your knowledge of Pythagorean Identities to solve the following problems.
1. |
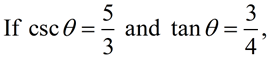find the values of the remaining trigonometric functions, using a Pythagorean Identity. |
|
|
|
2. |
Simplify the expression 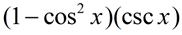 to a single trigonometric function. |
|
|
|
3. |
Simplify:  |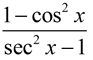
|
|
|
4. |
Simplify: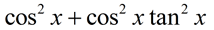 
|
|
|
|
5. |
Simplify: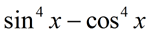 
|
|
|
|
6. |
Simplify this complex fraction into a single trigonometric function:
|
|
|
|
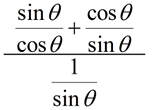
7. |
Write this expression as a monomial with a single trigonometric function: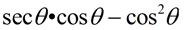 
|
|
|
|
8. |
Starting with sin2(x) + cos2(x) = 1, and using your knowledge of the quotient and reciprocal identities, derive an equivalent identity in terms of tan(x) and sec(x). Show all work.
|
|
|
|
9. |
Using the identity sin2θ + cos2θ = 1, find the value of tanθ , to the nearest hundredth, if cosθ equals -0.7 and θ is in Quadrant II.
|
|
|
|
10. |
Using a Pythagorean Identity, find sinθ if cosθ = ½ and θ terminates in Quadrant IV.
|
|
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
