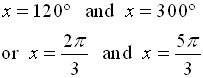|
Basic Trigonometric Equations: |
When asked to solve 2x - 1 = 0, we can easily get 2 x = 1 and x = 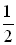 as the answer. When asked to solve 2sinx - 1 = 0, we proceed in a similar manner.
We first look at sinx as being the variable of the equation and solve as we did in the first example.
2sinx- 1 = 0
2 sinx = 1
sinx = 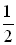 |
But this is only part of the answer. |
|
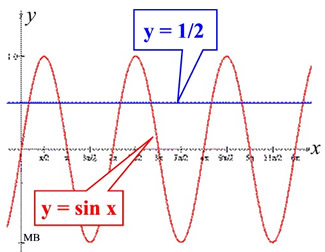
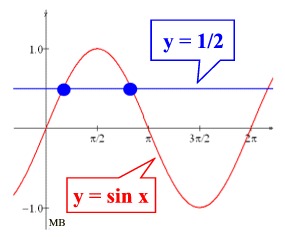
If we look at the graph of sinθ from 0 to 2π,
we will remember that there are actually
TWO values of θ for which the sinθ = 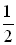 . .
These values are at:
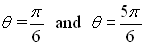
or at 30º and 150º. |
If we look at the extended graph of sinθ , we see that there are many other solutions to this equation sinθ = 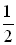 . .
We could arrive at these "other" solutions by adding a multiple of 2π to θ.
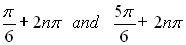
where n is an integer in [0,∞).
|
|
Most equations, however, limit the answers to trigonometric equations to the domain
[0, 2π] or [0º, 360º]. (Always read the question carefully to determine the given domain.) |

Solutions of trigonometric equations may also be found by examining
the sign of the trig value and determining the proper quadrant(s) for that value.
 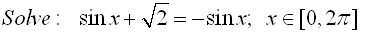
Solution: First, solve for sin x.
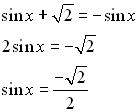
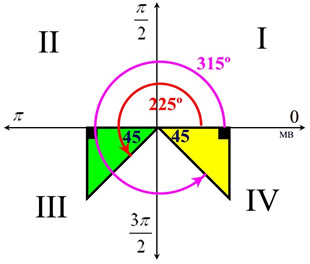
Now, sine is negative in Quadrant III and Quadrant IV. Also, a sine value of 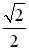 is a reference angle of 45º. So, consider the reference angle of 45º in quadrants III and IV. is a reference angle of 45º. So, consider the reference angle of 45º in quadrants III and IV.
|
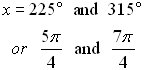 |
 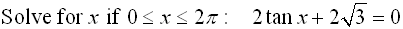
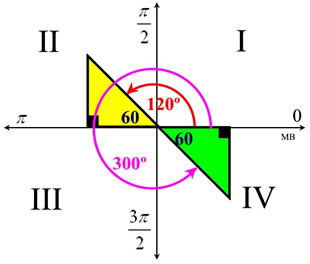
Solution: First, solve for tan x.
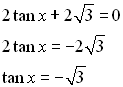
Now, tangent is negative in Quadrant II and Quadrant IV.
Also, a tangent value of 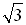 is a reference angle of 60 degrees. So, consider the reference angle of 60º in quadrants II and IV. is a reference angle of 60 degrees. So, consider the reference angle of 60º in quadrants II and IV.
|
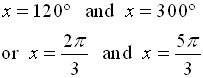 |

|
For help with trigonometric equations on
your calculator,
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
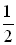 as the answer.
as the answer.
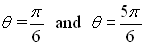
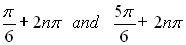

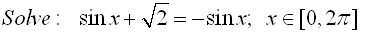
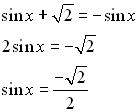
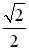 is a reference angle of 45º. So, consider the reference angle of 45º in quadrants III and IV.
is a reference angle of 45º. So, consider the reference angle of 45º in quadrants III and IV.
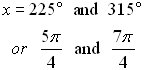
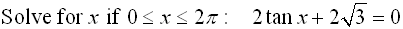
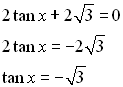
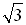 is a reference angle of 60 degrees. So, consider the reference angle of 60º in quadrants II and IV.
is a reference angle of 60 degrees. So, consider the reference angle of 60º in quadrants II and IV.