The symbols and notations used in statistics can get to be a bit confusing. One confusing factor is distinguishing between notations (symbols) that are used when dealing with "populations" and those used when dealing with "samples".
Let's look at "populations" versus "samples". |
 |
• Population refers to the complete set of observations that can be made.
If you are studying the heights of adult dogs, the population would be the set of the heights of all dogs in the world. If you are studying the height of adult dogs living in Connecticut, the population would be the set of the heights of all dogs living in Connecticut. "Populations" are generally difficult to study since they usually include extremely large numbers of potentially unavailable subjects. |
• Sample refers to a set of observations drawn from a population.
Samples are used when it is impractical to study entire populations due to the extremely large number (and accessibility) of the subjects. If you want to study the favorite songs of 17 year old American males, it will be impossible to survey EVERY 17 year old American male.
You can, however, survey a "sample" of 17 year old American males. |
Population |
μ refers to population mean
σ refers to population standard deviation
p refers to population proportion
N refers to population size |
A parameter is a fixed number that describes a population, such as a percentage, proportion, mean or standard deviation. In reality, we most likely do not know these numbers because we cannot examine the entire population. |
|
Sample |
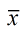 refers to sample mean refers to sample mean
s refers to sample standard deviation
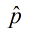 refers to sample proportion refers to sample proportion
n refers to sample size
|
A statistic is a known number that describes a sample, such as a percentage, proportion, mean or standard deviation, but it can change from sample to sample. A statistic is an estimate of a parameter. |
|
Placing a hat (or caret) over a parameter denotes an "estimator" of that parameter
(or the "predicted" value). 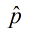 is called "p-hat" and is the proportion of a sample set which may be used to predict the proportion, p, of a larger population. is called "p-hat" and is the proportion of a sample set which may be used to predict the proportion, p, of a larger population.
When you first begin working with statistics, you use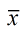 to represent "mean" since most work is done with samples, and to represent "mean" since most work is done with samples, and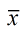 coordinates with your calculator symbol. coordinates with your calculator symbol. |