2. Situation: Finger tap rates with and without caffeine
Subjects: 20 male college students randomly divided into two groups of 10 in each group
Treatment: Each group drank two cups of coffee. One group was drinking coffee with 200 mg caffeine. The other group was drinking decaffeinated coffee.
Measurement: After two hours each student was |
|
tested to measure finger tapping rates (taps per minute).
Null Hypothesis: Caffeine does not produce an increase in the average tap rate.
Alternative Hypothesis: Caffeine produces an increase in the average tap rate.
Confidence Level: 95%
Hypothesis Method: Randomization Test
A Randomization Test on this data would require 20C10 = 184,756 re-samples.
A computer program will be used to model the randomization distribution for 1000 re-samples to give us approximate findings. (Dot plot from lock5stat.com applet.)
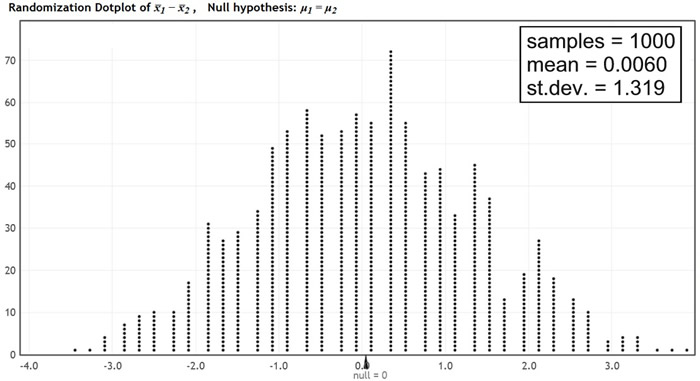
Observed data:
|
245 |
246 |
246 |
248 |
248 |
248 |
250 |
250 |
250 |
252 |
|
242 |
242 |
242 |
244 |
244 |
245 |
246 |
247 |
248 |
248 |
a) What are the means of the taps per minute for the two groups?
(caffeine group, no caffeine group)
Choose:
b) What is the difference of the means of the taps per minute for the observed data ("caffeine group - no caffeine group")?
Choose:
c) Using the information presented in this scenario, determine whether there is statistical significance in the difference of the means relating to taps per minute observed in this study. Justify your answer.