|
Directions: Grab paper and pencil to show your work as you find your solutions.
1. |
In 1798, economist Thomas Malthus proposed that the human population would grow geometrically,
(1, 2, 4, 8, 16, 32, ...),
while the production of food would grow arithmetically
(1, 2, 3, 4, 5, 6, ...).
|
|
| |
a) Prepare a scatter plot showing a comparison of a geometric growth to an arithmetic growth over 6 years, using the simple values given above.
b) What concept was Malthus trying to convey by this mathematical comparison of population growth to food production?
|
|
2. |
The Lyman Series of hydrogen is used to find energy levels at various spectral lines in a hydrogen atom. The formula for the series is given by the explicit sequence formula:
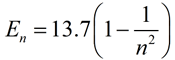 electron Volts (eV). electron Volts (eV).
Compute the energy in eV for the 4 th spectral line for a hydrogen atom.
|
Hydrogen spectrum:
the dark lines indicate wavelengths at which different energy levels, n, occur.
En is the energy measured in electron Volts at level n.
En follows a simple mathematical sequence.
Source: NASA |
|
3. |
The Sierpinski Triangle is a geometric pattern formed by connecting the midpoints of the sides of an equilateral triangle, and removing the new triangle formed.
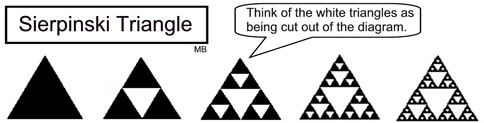
You can think of the diagram as an equilateral triangle being subdivided recursively into smaller equilateral triangles.
The Sierpinski Triangle is an example of a geometric representation of a geometric sequence. Let's establish a geometric sequence based upon the number of shaded triangles remaining in each stage of the process.
Find a recursive rule and an explicit rule for the number of shaded triangles remaining in the nth step of the process, referenced as an.
|
|
4. |
A professional football player signs a contract with a beginning salary of 3 million dollars for the first year and an annual increase of 5% per year beginning with year 2. To the nearest dollar, how much money will the player be paid over 5 years on this contract?
|
|
|
5. |
To play the Towers of Hanoi game, you must move the discs from peg A to peg B by moving one disc at a time. A larger disc can never sit atop a smaller disc. Peg C can be used as a holding area.
In the actual problem, there are a total of 64 discs.
|
|
| |
The number of moves needed to solve the game, based upon the number of discs in the game, can be expressed recursively.
Mn = the number of moves based upon the number of discs, n.
M1 = 1
Mn = 2Mn-1 + 1
a) How many moves are needed to solve the Towers of Hanoi using the discs shown in the diagram in this question.
b) There is another pattern (formula) developing in the number of moves required based upon the number of discs. Write an explicit formula for the number of moves based upon the number of discs.
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|