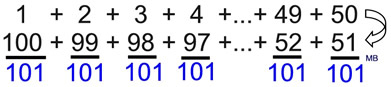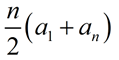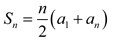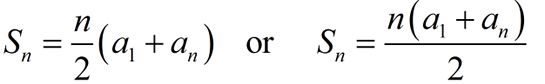Carl Friedrich Gauss (1777-1855) was a German mathematician who contributed in many fields of mathematics and science and is touted as one of history's most influential mathematicians.
As the story goes, when Gauss was a young boy, he was given the problem to add the integers from 1 to 100. Remember that there were no calculators in those days!
As the other students struggled with this lengthy addition problem, Gauss saw a different way to attack this problem. He listed the first 50 terms, and then listed the second fifty terms in reverse order beneath the first set. You can think of it as he "wrapped" the series back onto itself.
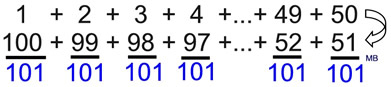
|
|
Gauss them added the paired values, noticing that the sums were all the same value (101).
Since he had 50 such pairs, he multiplied 101 times 50 and obtained the sum of the integers from 1 to 100 to be 5050.
Now, Gauss's discovery works nicely as long as you have an even number of terms in your series. But what happens to the "wrapped" pairings if the series has 25 terms? Well, Gauss' discovery would need a bit of tweaking. If the number of terms is odd, do not split the series in half. Simply list the ENTIRE series forward, then list the entire series in reverse and add the pairs. In this situation, you will need to multiply the sum by the number of pairs and then divide by two, since you are actually working with 2 complete series.
By observing the series from BOTH directions simultaneously, Gauss was able to quickly solve the problem and establish a relationship that we still use today when working with arithmetic series.
Let's generalize what Gauss actually did.
Consider the following:
a1 + a2 + a3 + . . . + an-1 + an |
Let's represent 1+2+3+...+100 in subscripted a notation |
a1 + an |
All of Gauss' wrapped pairs have a sum of 101. While any pair could be used, it will be easier if we choose the first pair on the left, the addition of the first and last term, as these terms are usually more readily available. |
|
Gauss multiplied this sum times 50, which is HALF the number of terms in his sequence. So, we need to multiply times half of the number of terms in the sequence, which is represented by n. Is this starting to look familiar? |
|
Thus, was born a formula for the sum of n terms of an arithmetic sequence. |
This relationship of examining a series forward and backward to determine the value of a series works for any arithmetic series.
You may see the formula written as:
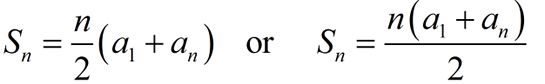
Sum, Sn, of n terms of an arithmetic series.
The first formula is Gauss' formula referencing n to be even.
The second formula is a more general formula implying n to be even or odd.
Algebraically, both formulas are equivalent.

Example 1: (Even Number of Terms) Find the sum of 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16.
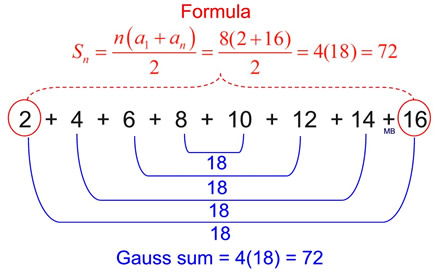

Example 2: (Odd Number of Terms) Find the sum of 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18.


 Why is Gauss' pairing up the terms in an arithmetic series
Why is Gauss' pairing up the terms in an arithmetic series
always giving the same sums?
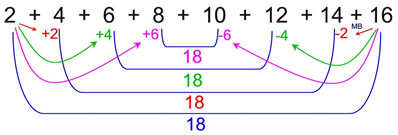
If you examine the graphic above, you can see that if you add the first and last terms you get 18.
If you add the second term to the seventh term you will also get 18 because you are +2 and -2 away from the first and last terms. Thus, you have moved +2 - 2 = 0 away from 18. Remember that in an arithmetic series, the common difference is constant and this pattern of adding and subtracting the same value as the terms are paired will continue. All sums will be 18.