|
Directions: Read carefully.
1. |
Find the sum of the first 20 terms of the arithmetic sequence: 4, 6, 8, 10, ...
Choose:
|
 |
|
2. |
Find the sum of an arithmetic sequence whose last term is
a10 = -26 and whose common difference is d = -4.
|
|
3. |
Find the sum of the arithmetic sequence -8, -5, -2, ..., 7.
|
|
4. |
Evaluate this series using a formula:
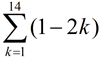 Choose:
Choose:
|
 |
|
5. |
Find the sum of the positive integers from 4 to 44 inclusive.
Choose:
|
|
|
6. |
A display of cans on a grocery shelf consists of 20 cans on the bottom, 18 cans in the next row, and so on in an arithmetic sequence, until the top row has only 4 cans. How many cans, in total, are in the display?
Choose:
|
 |
|
7. |
How many terms of the arithmetic sequence -3, 2, 7, ... must be added together for the sum of the series to be 116?
Choose:
|
|
|
8. |
Express the indicated sum in terms of n:
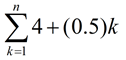 |
|
Choose:
|
|
|
|
9. |
Given: a1 = 3; an = an-1 - 4
Find the sum of the first 315 terms of this sequence.
|
|
| Choose:
|
|
|
|
10. |
The sum of the first three terms of an arithmetic sequence is 108, and the sum of the next three terms is 183. What is the value of the 11th term?
Choose:
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|