For a review on working with expressions, including simplifying, adding, subtracting,
multiplying, dividing, and domains, see the Refresher Sections at the bottom of the Topic Page.
As your work with rational expressions continues, you will find that the simplification of rational expressions will become more and more useful. A factored rational expression will give pertinent information about the expression, as related to an application, a graph, a design, etc. Such a factored form will be considered a "more desirable" form of the expression.
In Algebra 2, your work with rational expressions will be expanded.
Let's take a look at some of the types of problems you may be solving.


Rewrite the expression 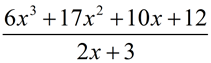 in keeping with
in keeping with 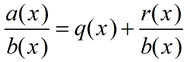 where a(x), b(x), q(x) and r(x) are polynomials and the
where a(x), b(x), q(x) and r(x) are polynomials and the
degree of r(x) is less than the degree of b(x).
Note: The rational expression in this problem is an improper rational expression (degree of top > degree of bottom). We know that improper fractions, such as 21/2, can be written as a mixed number, 10½, by dividing the denominator into the numerator, and "adding on" the remainder over the denominator. This same concept is occurring in this problem. We will be changing an improper rational expression into a "mixed" rational expression.
Answer:
This problem is asking you to divide the numerator by the denominator, and to write the answer as a quotient with a remainder.
You know how to accomplish this division, but perhaps you have not seen the question asked in this manner.
Note that this expression is undefined for the x-value of -3/2.
|
|


Explain if the simplification shown below is true, and whether there are any restrictions placed on the value of m: 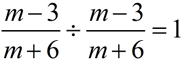
Answer:
This simplification is true since a value divided by itself equals one.
Yes, there are restrictions on m.
m ≠ -6 and m ≠ 3. Notice that when the second fraction is inverted, (x - 3) becomes a denominator which cannot be zero.
|
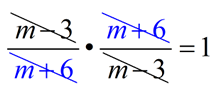
m ≠ -6 and m ≠ 3.
|

Show that the following statement is true. 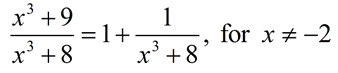
Answer:
When "showing" that a statement is true, be sure to include sufficient information to demonstrate that you understand what is happening, and why, in the problem.
Also, comment on the stated restriction.
|
By long division, it can be seen that the quotient is 1 and the remainder is 1. 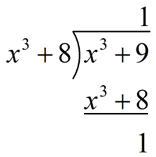
When the remainder is expressed over the divisor, the given statement is shown to be true. The restriction of x ≠ -2 is needed to prevent a zero denominator.
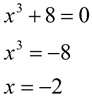
|


Combine and simplify: 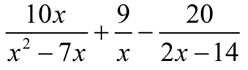 . Specify restriction(s).
. Specify restriction(s).
Answer:
Factor where possible.
x2 - 7x = x(x - 7)
2x - 14 = 2(x - 7)
Find the common denominator for the three denominators, which is 2x(x - 7).
Adjust the numerators to accommodate the new denominators. Add and subtract.
Then simplify.
Be sure to include restrictions that would apply to all of the three initial fractions.
|
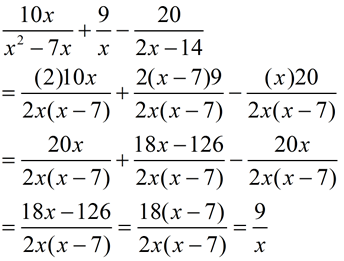 Restrictions: x ≠ 0, x ≠ 7
Restrictions: x ≠ 0, x ≠ 7
|


Combine and simplify: 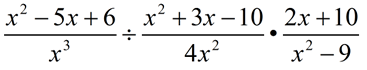 . Specify restriction(s).
. Specify restriction(s).
Answer:
Factor where possible.
x2 - 5x + 6 = (x - 3)(x - 2)
x2 + 3x - 10 = (x + 5)(x - 2)
2x + 10 = 2(x + 5)
x2 - 9 = (x + 3)(x - 3)
Invert the term to be divided.
Reduce (and cancel) top expressions with bottom expressions.
Specify restrictions based upon the initial fractions and the inverted division fraction.
|
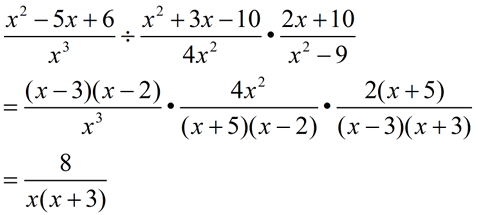
Restrictions: x ≠ 0, x ≠ ±3, x ≠ 2, x ≠ -5
|