To MUTLIPLY rational expressions:
Factor first, reduce, and then multiply through.
Always reduce a factor from the top with a factor from the bottom! |
 Steps to Multiplying Rational Expressions: Steps to Multiplying Rational Expressions:
Your teacher may, or may not, ask you to state the domains of rational expressions.
1. Factor first, if possible.
There is no factoring to be done first in this example,
Reduce the expression using your knowledge of the properties of exponents.
If a problem looks confusing, a listing of the individual factors may be helpful for seeing what can be reduced.
|
|
2. Multiply through the numerator and multiply through the denominator.
Check to see if the final answer can be reduced further, in case you did not reduce all factors prior to multiplying. |
2. 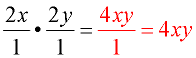 Ans. Ans.
Domain: x ≠ 0; y ≠ 0
|
 Examples: Examples:
Example 1:
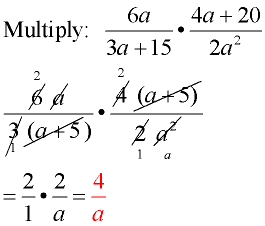
Domain: a ≠ 0,
a ≠ -5
|
Factor first.
Reduce common factors.
 Do NOT reduce single terms from within parentheses containing a "+" or "-" sign. Reduce the entire parentheses. Do NOT reduce single terms from within parentheses containing a "+" or "-" sign. Reduce the entire parentheses.
State the domain if so directed by the problem or by your teacher.
|
| |
Example 2:
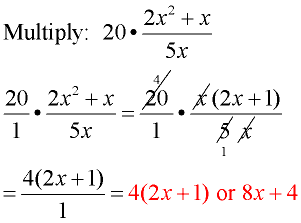 Domain: x ≠ 0
Domain: x ≠ 0
|
Multiplying by 20 is the same as multiplying
by 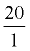 . . Writing 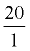 may make the process more observable.
Factor the numerator of the fraction.
Reduce common factors.
State the answer as directed by your teacher.
|
| |
Example 3:
Multiply: 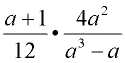
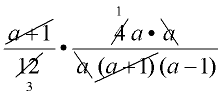
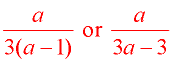
Domain: a ≠ -1, 0, 1
|
Factor first.
The denominator of the second fraction factors:
a3 - a = a(a2 - 1) = a(a + 1)(a - 1)
Reduce common factors (top with bottom).
Express your final answer in the form desired by your teacher, or by the form that may be stated in the problem (such as "in simplest form" or "in simplest factored form"). |

To DIVIDE rational expressions:
Flip second fraction, factor, reduce, multiply through.
Always reduce a factor from the top with a factor from the bottom! |
 Steps to Dividing Rational Expressions: Steps to Dividing Rational Expressions:
Your teacher may, or may not, ask you to state the domains of rational expressions.
1. Invert (flip) the second fraction, and change the division sign to multiply.
Just as you do when dividing numerical fractions, you need to take the reciprocal ( invert, flip) the second fraction and then multiply.
Note the domain of the original problem.
|
1.
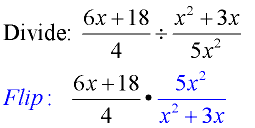
Domain: x ≠ 0 |
2. Factor, if possible.
Reduce a factor from the numerator with a factor from the denominator.
Reduce entire parentheses.
|
2. 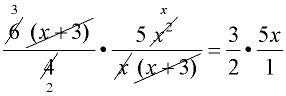 |
3. Multiply through the numerator and multiply through the denominator.
Check if any further reducing may be possible.
|
3. 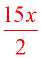 Ans. Ans.
Domain: x ≠ 0
|
 Examples: Examples:
Example 1:
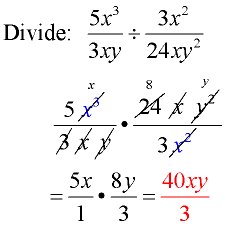
Domain: x ≠ 0, y ≠ 0
|
Flip second fraction and change division sign to multiply.
Factor.
Reduce common factors.
This example shows one way to reduce the factors.
State the domain if so directed by the problem or by your teacher.
|
| |
Example 2:
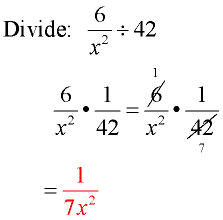 Domain: x ≠ 0
Domain: x ≠ 0
|
Remember that 42 is really 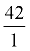 . .
Flip second fraction and change to multiplication.
Factor and reduce common factors.
|
| |
Example 3:
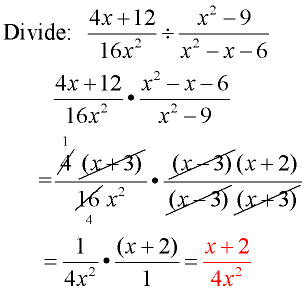 Domain: x ≠ 0; x ≠ 3; x ≠ -2
Domain: x ≠ 0; x ≠ 3; x ≠ -2
|
Flip second fraction and change to multiplication.
Factor.
Reduce common factors.
Be careful to reduce entire parentheses.
State the answer as directed by your teacher.
|
|