|
A rational inequality is an inequality which contains a rational expression. |
The trick to dealing with rational inequalities is to always work with zero on one side of the inequality. Re-write the problem if necessary to obtain a zero on one side!
Then ... the x-values that make the numerator zero and
the x-values that make the denominator zero (undefined) will determine the number line test values.
A rational expression changes its sign only at its zeros and its undefined values. |
 Solving Rational Inequalities: (Method 1 is the preferred method for this course.) Solving Rational Inequalities: (Method 1 is the preferred method for this course.)
Method 1: Find the number line test intervals and test each interval
(a graphical approach) |
1. If necessary, rewrite the inequality so a zero appears on one side, with a single fraction on the other side.
2. Find the x-value(s) that make the numerator equal to zero.
3. Find the x-value(s) that make the denominator equal to zero.
The values from steps 2 and 3 will determine the number line test intervals.
4. On a number line, mark each of the values from steps 2 and 3.
Use only these values to create intervals on the number line.
5. Select a test point in each interval, and check to see if that test point satisfies
the original inequality. (This will determine the intervals which satisfy the inequality.)
6. Mark the number line to reflect the values and intervals that satisfy the inequality.
7. State your answer using the desired form of notation. |

 Solve: Solve: 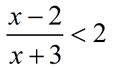
1. Rewrite the inequality to contain a zero on the right-hand side. Create a single fraction on the left-hand side.
|
Subtract the 2 from both sides. Get common denominator on the left side.
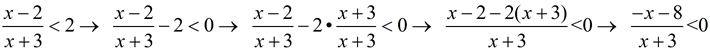 |
| 2. Determine any value(s) that makes the numerator equal 0. |
-x - 8 = 0 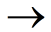 x = -8 x = -8 |
3. Determine any value(s) that makes the denominator equal 0.
|
x + 3 = 0 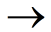 x = -3 x = -3 |
4. Prepare number line using only values from steps 2 and 3 as your marked values. |
|
5. and 6. Select a test point in each interval and check to see if it satisfies the original inequality, or the inequality set < 0. (The original inequality is used in the chart below.) Mark the number line with arrows/segments, and label TRUE/FALSE. |
test point -9:
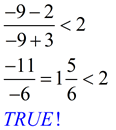 |
test point -5:
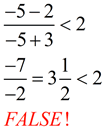
|
test point 0: 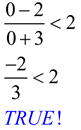 |

|
| 7. State answer. |
|
 It may appear from the example above that the "truth values" on the number line will alternate back and forth between TRUE and FALSE along the line. This is NOT necessarily the case. You may run into a pattern of FALSE, TRUE, TRUE (or any other combination) along the line. It may appear from the example above that the "truth values" on the number line will alternate back and forth between TRUE and FALSE along the line. This is NOT necessarily the case. You may run into a pattern of FALSE, TRUE, TRUE (or any other combination) along the line. |
|
RE: Alternate way to find the "numerator" critical value(s)
In the original inequality, if you change the inequality symbol to an equal sign
and then solve the inequality for x, you will obtain the same critical value(s) that you got from the numerator set = 0.
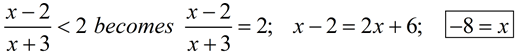
|

| Method 2: Find critical values by algebraic reasoning (formal algebraic approach) |
For this discussion, a = the numerator and b = the denominator.
1. If necessary, rewrite the inequality so a zero appears on one side, with a single fraction on the other side.
2. If a / b > 0, then either a > 0 and b > 0 OR a < 0 and b < 0.
(a and b are both positive or both negative)
If a / b < 0,
then either a > 0 and b < 0 OR a < 0 and b > 0.
(a and b are one positive and the other negative) |
|
3. Create inequalities where a and b meet the conditions of the situation.
4. Determine x-values that make the denominator zero, and check to see if this condition has already been met.
5. State your answer using the desired form of notation. |

 Solve: Solve: 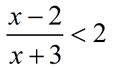
1. Rewrite the inequality to contain a zero on the right-hand side. |
Subtract the 2 from both sides. Get common denominator on the left side.
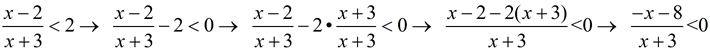 |
| 2. Determine the situation associated with this inequality. |
Since this inequality is < 0, the situation is "If a / b < 0,
then either a > 0 and b < 0
OR a < 0 and b > 0.
|
3. Create inequalities where a and b meet the conditions of the situation. |
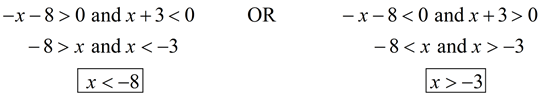
Remember, the word "and" means BOTH conditions must be true at the same time. |
| 4. Determine x-values that make the denominator zero. |
x + 3 = 0  x = -3 gives a zero denomiator. So x ≠-3. This is already taken care of in step 3, with x > -3. x = -3 gives a zero denomiator. So x ≠-3. This is already taken care of in step 3, with x > -3. |
| 5. State answer. |
|
|