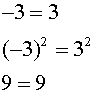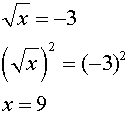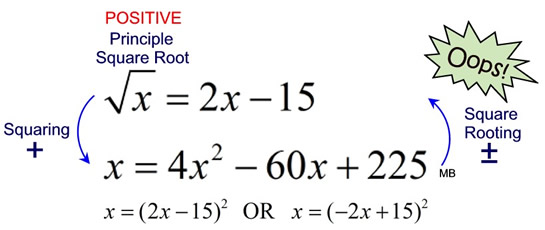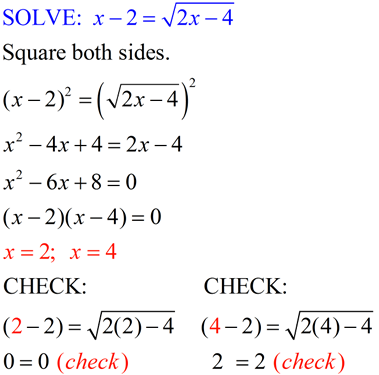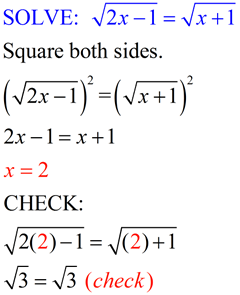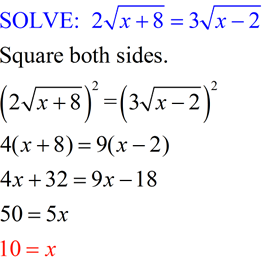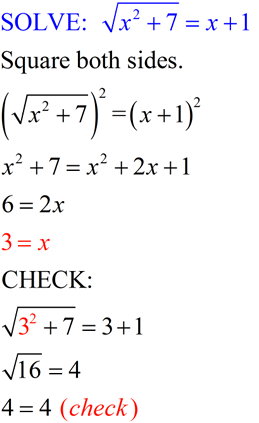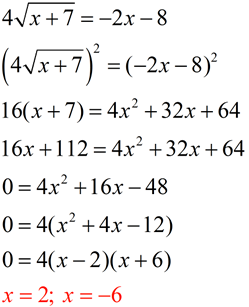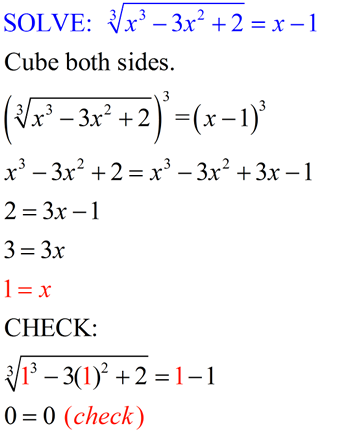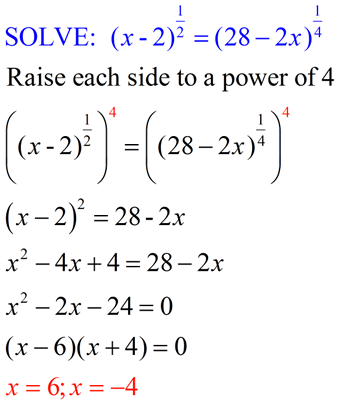On this page, all radicals and expressions with rational exponents represent real numbers.
The "radical" in a radical equation may be of any root value: square root, cube root, fourth root, etc. This page will concentrate on working with "square root" equations.
 |
Remember that a radical equation has the variable "under" the radical, not simply a numerical radical value within the equation.
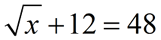 is a radical equation
is a radical equation |
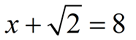 is NOT a radical equation
is NOT a radical equation |
|
|
The solution to a radical equation is a real number which, when substituted for the variable, yields a true equation. Radical equations with square roots can be solved by "squaring", with cube roots by "cubing", and so on. This solution process is an application of the principle:
If a and b are real numbers, n is a positive integer, and a = b, then an = bn. |
The solutions, however, get significantly "messier" to find as the indexes increase.
To solve radical equations:
| 1. |
Isolate the radical (or one of the radicals) to one side of the equal sign. |
| 2. |
If the radical is a square root, square each side of the equations. If the radical is not a square root, raise each side to a power equal to the index of the root. |
| 3. |
Solve the resulting equation. |
| 4. |
Check your answer(s) to avoid extraneous roots. |
|
|
Square "sides", not "terms".
|
SIDES:
2 + 4 = 6
(2 + 4)² = 6²
36 = 36 |
TERMS:
2 + 4 = 6
2² + 4² ≠ 6²
4 + 16 ≠36 |
 |
How to use your
TI-83+/84+
calculator
with
radical equations.
Click here. |
|
|

The process of squaring the sides of an equation creates a "derived" equation which may not be equivalent to the original radical equation. Consequently, this new derived equation may create solutions that never previously existed. These "extra" roots that are not true solutions of the original radical equation are called extraneous roots and are rejected as answers.
The first statement is false, but when each side is squared, the concluding statement is true.
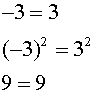
|
|
The first statement is false, but when each side is squared, the concluding statement is true.
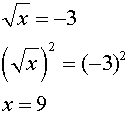
|
|
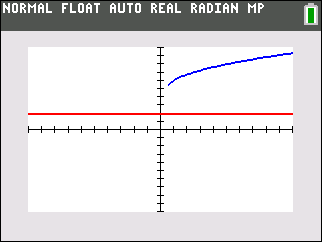
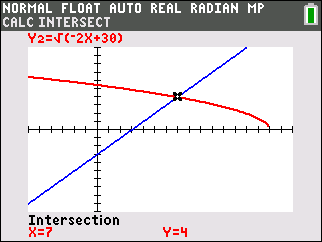
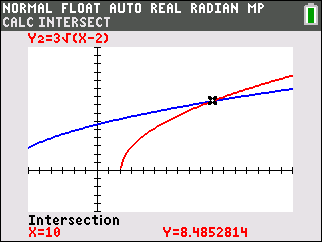
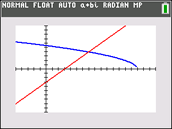
Let's look at this problem of extraneous roots visually. Consider the example from above of 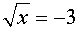
There is NO solution to this equation since the graphs of the two sides (components) of the equation do not intersect.
Squaring both sides, however, creates an equation with two sides, that when graphed, DO intersect, leading to a false answer.
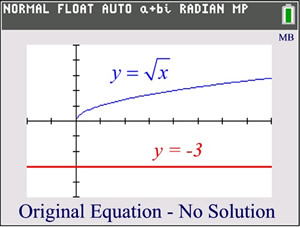
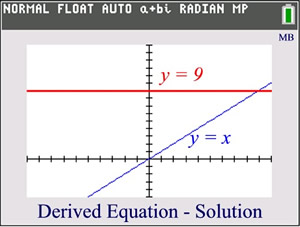
Keep in mind that some of these "perceived" solutions may not actually work when plugged back into the original equations.
This problem arises from the fact that the converse of the statement:
If a and b are real numbers, n is a positive integer,
and a = b, then an = bn.
is true when n is odd, but not necessarily true when n is even.
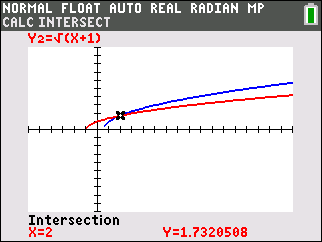
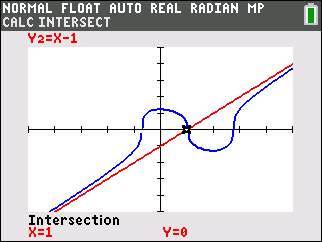
Let's examine another square root situation shown below. We can square both sides of the first radical equation and obtain a true quadratic equation. This new quadratic equation contains not only the square of (2x - 15), but can also contain the square of (-2x + 15), which we do not want. If we take the square root of both sides of the new quadratic equation, we will get two interpretations, 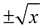 . The new derived equation is yielding more information than we need by offering up extraneous root solutions.
. The new derived equation is yielding more information than we need by offering up extraneous root solutions.
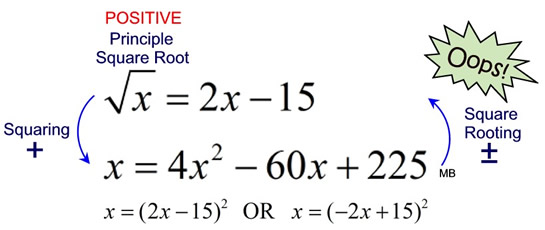
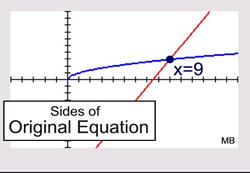
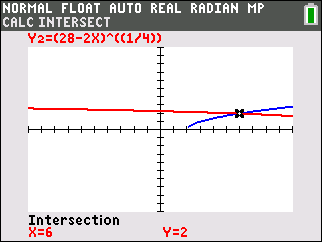
Notice how the graph of the sides of the original radical equation show ONE solution.
The graph of the new equation shows TWO solutions. The solution of x = 6.25 will not check in the radical equation. |
|
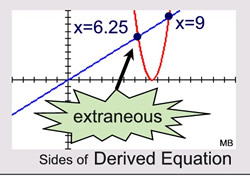 x = 4x2 - 60x + 225
x = 4x2 - 60x + 225 |
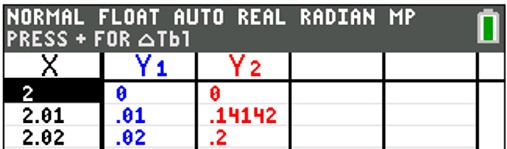
CHECKING will be essential to finding correct solutions
(and catching these pesky extraneous roots).
 |
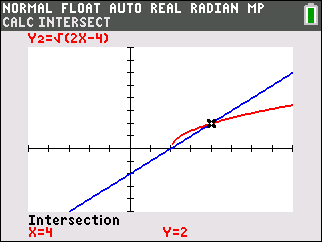
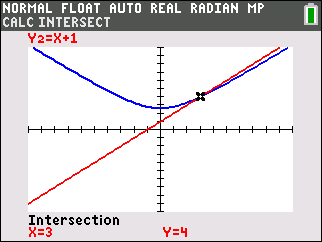
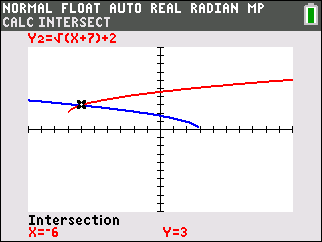
How many correct solutions will a radical equation have?
Grab your graphing calculator.
Graph each side of the equation and look for intersections.
With 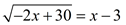 there is ONE intersection, meaning ONE solution. The algebraic solution will show TWO, one of which will be extraneous. there is ONE intersection, meaning ONE solution. The algebraic solution will show TWO, one of which will be extraneous. |
 |
|

 Example where the answer checks!
Example where the answer checks!
 |
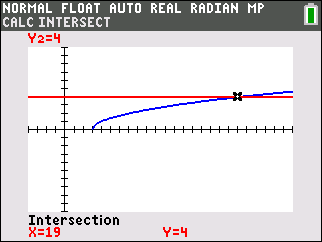 ANSWER: x = 19 ANSWER: x = 19
|