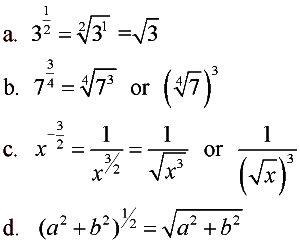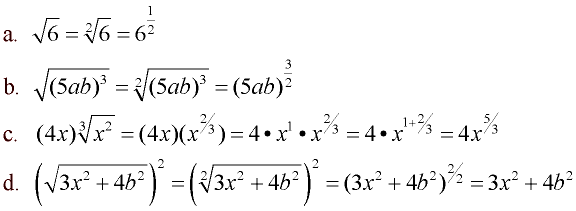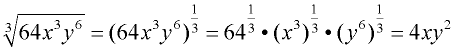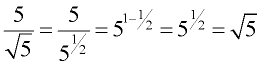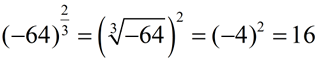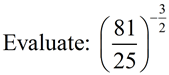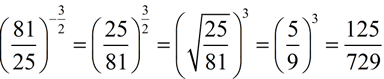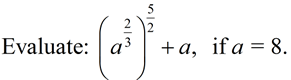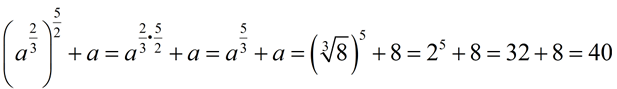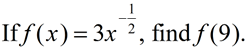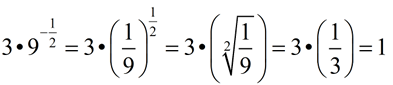|
As we have seen, a radical expression can be written in an equivalent form using a fractional (rational) exponent instead of a radical symbol. It is often easier to write and to manipulate an expression with a fractional exponent than one written in radical form. Let's take a further look into radicals and exponents.
|
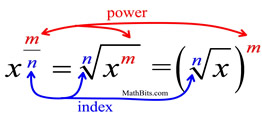
Fractional (rational) exponents are an alternate way to express radicals. If x is a real number and m and n are positive integers:
|
|
|
|
The denominator of the fractional exponent becomes the index (root) of the radical. The numerator of the fractional exponent becomes the power of the value under the radical symbol OR the power of the entire radical. |
Why TWO
possible results? |
If we apply the rules of exponents, we can see how there are two possible ways to convert an expression with a fractional exponent into an expression in radical form.
|
|
|

The exponent of 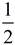 means the second root, or the square root: means the second root, or the square root: 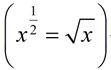 . .
The exponent of 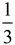 means the third root, or the cube root: means the third root, or the cube root: 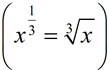 . .
And so on ...

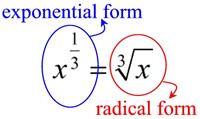
Remember:
All RULES that apply to exponents, also apply to fractional exponents! |
 Convert from Exponential to Radical Form: Convert from Exponential to Radical Form: |
|
Remember the denominator of the fractional exponent will become the root of the radical, and the numerator will become the power.
Create the power first and then the root.
OR
Create the root first and then the power.
Either way, you will have a correct answer. |
 Convert from Radical to Exponential Form: Convert from Radical to Exponential Form: |
Remember the index (root) of the radical will become the denominator of the fractional exponent, and the power will become the numerator.
Create the denominator first and then the numerator.
OR
Create the numerator first and then the denominator.
Either way, you will have a correct answer.
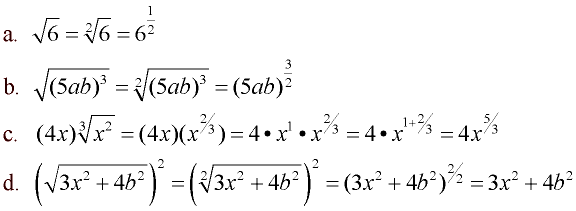 Notice in the last example, that raising a square root to a power of 2 removes the radical.
Notice in the last example, that raising a square root to a power of 2 removes the radical.
Squaring and square rooting are inverse operations. One undoes the other.
|
 |
When simplifying radicals, it is often easier to find the answer by first rewriting the radical with fractional exponents. Let's see two examples:
1. 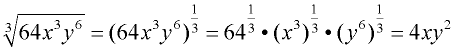 2.
2. 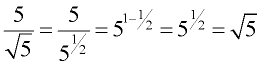 |


NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

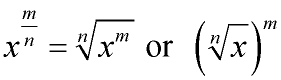
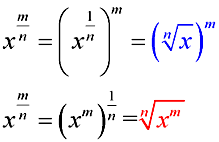
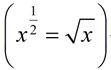 .
.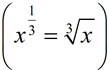 .
.