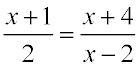|
Solving a Quadratic Equation: ax2 + bx +c = 0
(For this unit, use of the word "trinomial" will imply the form ax2 + bx + c.)
| Method: Factoring Trinomials |
 To solve a quadratic equation by factoring. To solve a quadratic equation by factoring.
| |
Factoring Method |
1. |
Express the equation in the form ax2 + bx + c = 0. |
2. |
Factor the left hand side (if 0 is on the right). |
3. |
Set each of the two factors equal to zero. |
4. |
Solve for x to determine the roots (or zeros of graph). |
|
Simple quadratic equations with rational roots can be solved by factoring. Let's refresh our memories on factoring these simple factorable quadratic equations as they appear in different situations.
|
Note: Factoring by "Trial and Error" for a = 1 and a ≠ 1 can be found in Algebra 1. Algebra 2 will use other options.
Examples of Solving Quadratic Equations by Factoring:
Factoring with GCF
(greatest common factor):
|
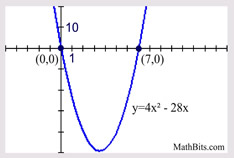
Solve: 4x2 - 28x = 0
4x(x - 7) = 0
4x = 0; x - 7 = 0
x = 0; x = 7
Always look for a GCF, to make the factoring easier.
|
|
Find the largest value which can be factored from each term on the left side of the quadratic equation.
The roots correspond to the locations of the x-intercepts (the zeros) of the function
|y = 4x2 - 28x. |
Factoring Trinomial with Leading Coefficient of One:
|
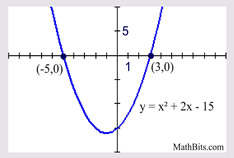
Solve: x2 + 2x - 15 = 0
(x + 5)(x - 3) = 0
x + 5 = 0; x - 3 = 0
x = -5; x = 3
Pattern:
x2 + (m+n)x + m•n = (x+m)(x+n) |
|
When the leading coefficient is one, the product of the roots will be the constant term, and the sum the roots will be the coefficient of the middle x-term. |
Factoring Perfect Square Trinomials:
|
Solve: x2 + 12x + 36 = 0
(x + 6)(x + 6) = 0
x + 6 = 0; x + 6 = 0
x = -6 (repeated root)
Pattern:
Both a2 and b2 are perfect squares, and (a ± b) = twice the product of a and b.
|
|
• (a + b)2 = a2 + 2ab + b2
• (a - b)2 = a2 - 2ab + b2
Noticing these patterns will help factor problems more quickly.
Be aware of the signs.
|
Factoring Trinomial - Leading Coefficient of One in Hiding:
|
Solve: 3x2 - 3x - 36 = 0
3(x2 - x - 12) = 0
3(x - 4)(x + 3) = 0
x - 4 = 0; x + 3 = 0
x = 4; x = -3
|
|
A leading coefficient of one may be "hiding". Look for a common factor of the coefficient of x2 to uncover a possible trinomial with a leading coefficient of 1. |
Factoring Difference of Two Squares:
|
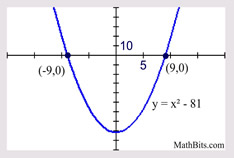
Solve: x2 - 81 = 0
(x + 9)(x - 9) = 0
x + 9 = 0; x - 9 = 0
x = -9; x = 9
Pattern:
a2 - b2 = (a + b)(a - b)
|
|
Remember the "pattern" for the difference of two squares, where the factors are identical except for the sign between the terms, forming a binomial conjugate pair.
|
Factoring Trinomial with Leading Coefficient Not One:
|
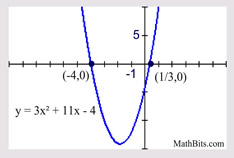
Solve: 3x2 + 11x - 4 = 0
(3x - 1)(x + 4) = 0
3x - 1 = 0; x + 4 = 0
x = 1/3; x = -4
Pattern:
ax2 + bx + c = (kx + m)(lx + n)
= klx2 + (kn + lm)x + mn
k and l are factors of a
m and n are factors of c
|
|
Factoring becomes more difficult when the leading coefficient is not one.
Check out the " ac Method & Factoring by Grouping" under Quadratics,
|
Where's the x2 ?
|
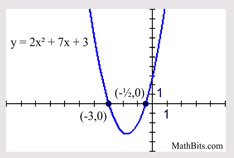
Solve: 2x(x + 4) = x - 3
2x2 + 8x = x - 3
2x2 + 7x + 3 = 0
(2x + 1)(x + 3) = 0
2x + 1 = 0; x + 3 = 0
x = - 1/2; x = -3
|
|
Sometimes you have to "work" on the equation to get the needed quadratic form. In this case, distribute, and the x2 will appear. |
Dealing with Proportions:
|
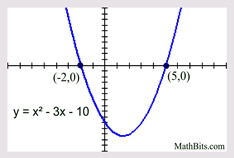
Solve: 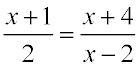
2( x + 4) = ( x + 1)( x - 2)
2 x + 8 = x2 - x - 2
0 = x2 - 3 x - 10
0 = ( x - 5)( x + 2)
x - 5 = 0; x + 2 = 0
x = 5; x = -2
|
|
x2 may appear when cross multiplying ("product of the means equals product of the extremes") is employed in a proportion. |
There are tools in this unit that are more powerful for solving difficult factorable quadratic equations
and for solving quadratic equations that are not factorable.

|
For
calculator help with solve
quadratic
equations 1.
click here. |
|
|
|
For
calculator help
with solve
quadratic
equations 2
click here. |
|
|
|
For calculator help with solve
quadratic
equations
click here. |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|