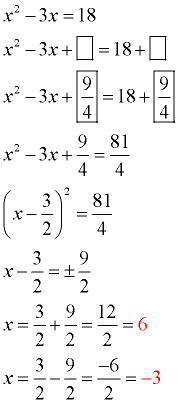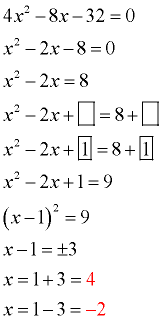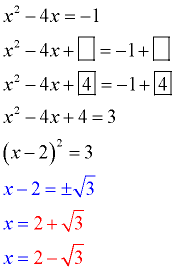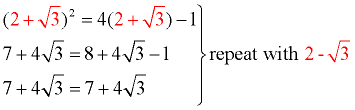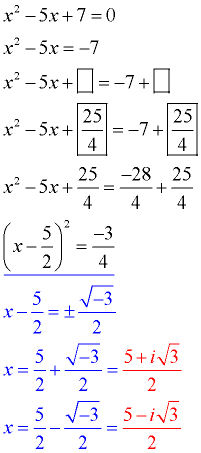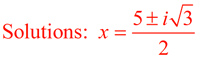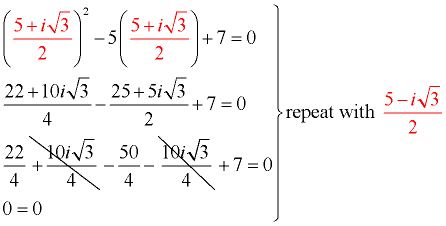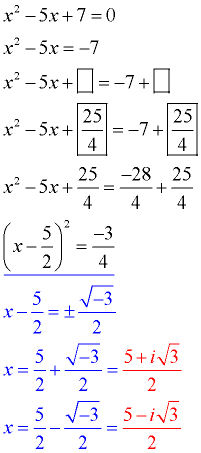
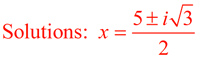
Notice that this example involves the imaginary "i", and has complex roots of the form a + bi.
Answers written in a + bi form:
Read more about imaginary values.
These answers are not "real number" solutions. They do not have a place on the x-axis. |
(The leading coefficient is one.) Move the constant to the right hand side.
Prepare the equation to receive the added value (boxes).
Take half of the x-term's coefficient and square it. Add this value to both sides (fill the boxes).
Get a common denominator on the right.
Factor the perfect square trinomial on the left side. Combine terms on the right.
 At this point, you have a squared value on the left, equal to a negative number. We know that it is not possible for a "real" number to be squared and equal a negative number. At this point, you have a squared value on the left, equal to a negative number. We know that it is not possible for a "real" number to be squared and equal a negative number.
____________________________________________
This problem involves "imaginary" numbers.
Take the square root of both sides. Be sure to consider "plus and minus". Notice the negative under the radical.
Solve for x. 
Prepare a check of the answers.
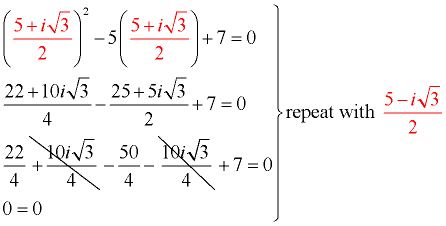 |