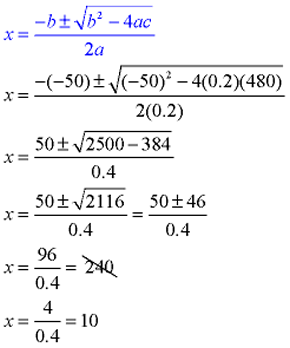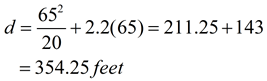|
We have seen that quadratic functions can be used to model projectile motion.
College professors Budd and Sangwin, in their article "101 Uses of a Quadratic Equation", state that "... the quadratic equation has played a pivotal part in not only the whole of human civilization as we know it, but in the possible detection of other alien civilizations and even such vital modern activities as watching satellite television."
(+plus magazine.org)
Let's take a look at a few of the other situations that may employ quadratic equations.
 Quadratic equations often occur in problems dealing with area. Quadratic equations often occur in problems dealing with area.
The llama rancher needs to fence two small adjacent rectangular pens as shown below. He has 100 feet of fencing and wants the pens to cover 350 square feet. Find the possible dimensions for measurements a and b in the diagram. |
Solution:
Let 2a = the total length
b = the width
4a + 3b = fence lengths = 100 feet
2ab = area = 350 square feet
Solve one formula for a or b:
4a + 3b = 100
a = (100 - 3b)/4 = 25 - 3b/4
Substitute into the other formula:
2ab = 350
2(25 - 3b/4)b = 350
50b - ½ (3b2) = 350
100b - 3b2 = 700
0 = 3b2 - 100b + 700
0 = (3b - 70)(b - 10)
3b - 70 = 0; b - 10 = 0
b = 70/3; b = 10
|

The rancher has two choices.
The values of a and b can be:
(1) b = 10 feet and a = 17.5 feet or
(2) b = 70/3 feet and a = 7.5 feet
|
 Quadratic equations often occur in problems with right triangles. Quadratic equations often occur in problems with right triangles.
The Adams' family home sits on a corner lot. Children cut across the corner from point B to point A (the front gate opening) rather than walking around the fence from B to C to A. Angle BCA is a right angle, AC = BC + 21 feet, and AB = BC + 24 feet. How many feet does a child save by cutting across the yard instead of walking around the corner?
|
Solution:
Let x = BC, the shorter leg
x + 21 = AC, the longer leg
x + 24 = AB, the hypotenuse
Apply the Pythagorean Theorem
a2 + b2 = c2
x2 + (x + 21)2 = (x + 24)2
x2 + x2 + 42x + 441 = x2 + 48x + 576
2x2+ 42x + 441 = x2 + 48x + 576
x2 - 6x - 135 = 0
(x - 15)(x + 9) = 0
x - 15 = 0; x = 15
x + 9 = 0; x = -9 (reject as lengths are not negative)
x = 15
x + 21 = 36
x + 24 = 39
AB = 39 feet
AC + BC =
36 + 15 = 51 feet
A child saves 12 feet by cutting across.
|

Check
in Pythagorean Theorem:
152 + 362 = 392
225 + 1296 = 1521
1521 = 1521 check
|
 Quadratic equations may be applied to financial situations. Quadratic equations may be applied to financial situations.
A store's revenue from selling skateboards is determined by multiplying the number of skateboards by the cost per skateboard. The revenue, r, from selling x skateboards (where x is less than or equal to 50) is r = x(50 - 0.2x). How many skateboards need to be sold to have a revenue of $480. |
When a formula (equation) is given within the problem, use the formula.
The problem generally requires you to substitute values into the formula and solve for some value.
Solution:
Set the formula equal to $480.
480 = x(50 - 0.2x)
480 = 50x - 0.2x2
0.2x2 - 50x + 480 = 0 (use quadratic formula)
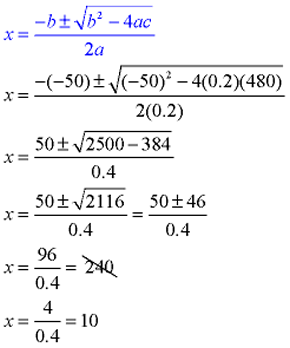
|

Since the problem stated that x was less than or equal to 50, reject the solution of 240.
They must sell 10 skateboards to have a revenue of $480. |
 Quadratic equations can apply to acceleration. Quadratic equations can apply to acceleration.
The braking distance, in feet, of a car traveling at v miles per hour is given by the equation: 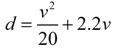 , where d is the braking distance and v is the velocity (speed) of the car (plus an allowance of 1.5 seconds for driver reaction time). If your car is traveling at 65 miles per hour, what distance is required to stop the car? |
Solution:
Replace v with 65 mph.
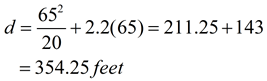
It will take you approximately the length of a football field (360 feet) to stop the car.
|

|
 Quadratic equations are used by NASA to achieve weightlessness. Quadratic equations are used by NASA to achieve weightlessness.
In preparing astronauts for space travel, and for conducting other experiments, NASA uses a C-9 jet to create short periods of weightlessness or near zero gravity, called microgravity. The jet sharply rises and falls in altitude following the arc of a parabola to create the weightlessness phenomena. Only the parabolic portion of the jet's flight will create this microgravity effect. During one such flight, the jet's parabolic ascent began at 30,000 feet and was modeled by the equation h = -16t2 + 350t + 30000 where h = altitude in feet and t = time in seconds.
a) How long did the
microgravity effect last?
b) What was the maximum altitude reached during this parabolic portion of the flight? |
Solution (algebraic):
h = -16t2 + 350t + 30000
a) Considering 30,000 feet to be the starting, and the ending, height of the parabolic arc, set h = 30,000 to find the ending time.
30000 = -16t2 + 350t + 30000
0 =
-16t2 + 350t
0 = t(-16t + 350)
t = 0 seconds; t = 21.875 seconds (ending time)
|
 Physicist Stephen Hawking
Physicist Stephen Hawking
experiencing near zero gravity. |
| b) The maximum height will be reached at the vertex of the parabola which will be half way between the starting time, t = 0, and the ending time, t = 21.875, or at 10.9375 seconds. We could also have used the axis of symmetry to find the t-coordinate for the vertex (-b/2a = -350/-32 = 10.9375). In either case, the height reached when t = 10.9375 is 31914.0625 feet (the maximum altitude reached). |
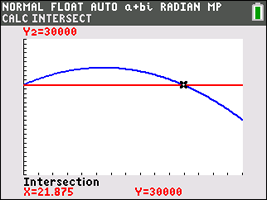 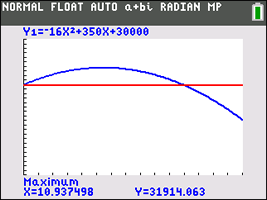 
The TI-84+ graphing calculator reinforces our findings, using the "intersection" option and the "maximum" option.
|
We will investigate more applications of quadratics
when we look at applied uses of parabolas as conics.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|