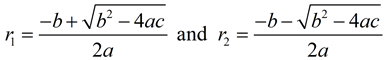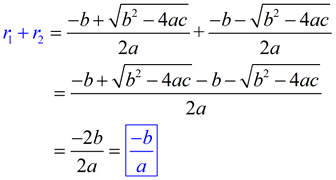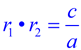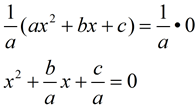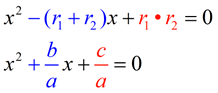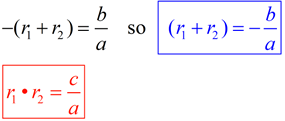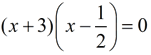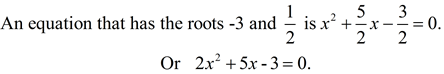|
We have seen that the b2 - 4ac portion of the quadratic formula, called the discriminant, can tell us the type of roots of a quadratic equation. The quadratic formula can also give us information about the relationship between the roots and the coefficient of the second term and the constant of the equation itself. Consider the following:
Given a quadratic equation: ax2 + bx + c = 0
By the quadratic formulas, the two roots can be represented as 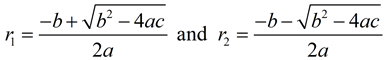
Sum of the Roots, r1 + r2:
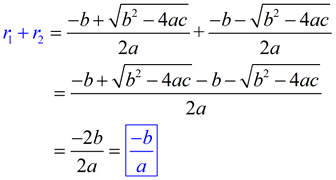
|
Product of the Roots, r1 • r2:

|
The sum of the roots of a quadratic equation is equal to the negation of the coefficient of the second term, divided by the leading coefficient. 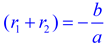
The product of the roots of a quadratic equation is equal to the constant term (the third term),
divided by the leading coefficient. 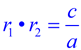 You will discover in future courses, that these types of relationships also extend to equations of higher degrees.
You will discover in future courses, that these types of relationships also extend to equations of higher degrees. |

We can also see these relationships emerge from factoring the quadratic equation.
The roots will be represented as r1 and r2.
Let's put this new information to work:
|
Yes, this question can be answered by simply multiplying the factors formed by these roots:
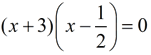
|
But, let's put our new formulas to use and apply the relationship between the roots and the coefficients and constants. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|