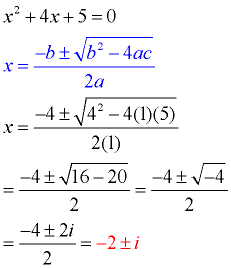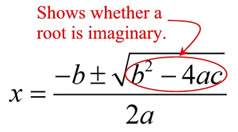|
In the section Complex Numbers, we started an investigation of the relationship between imaginary numbers (complex roots) and quadratic equations. Let's take a closer look.
 Quadratic Equations and Roots Containing "i ": Quadratic Equations and Roots Containing "i ":
In relation to quadratic equations, imaginary numbers (and complex roots) occur when the value under the radical portion of the quadratic formula is negative.
When this occurs, the equation has no roots in the set of Real numbers. The roots belong to the set of complex numbers, and will be called "complex roots" (or "imaginary roots"). These complex roots will be expressed in the form a ± bi.
 |
A quadratic equation is of the form ax2 + bx + c = 0 where a, b and c are real number values with a not equal to zero. |
|
Consider this example:
Find the roots: x2 + 4x + 5 = 0
This quadratic equation is not factorable, so we apply the quadratic formula. Notice that after combining the values, we are left with a negative value under the square root symbol (the radicand). This negative square root creates an imaginary number (a number containing "i ").
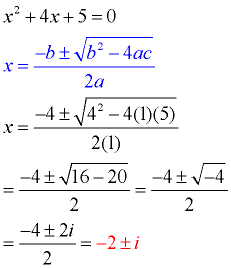
|
Since there were no real roots for the equation,
there will be no real zeros for the graph. 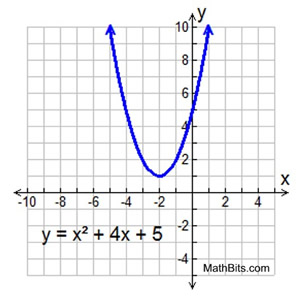 The graph of this quadratic function shows that there are no real zeros because the graph does not cross the x-axis. Such a graph tells us that the roots of the equation are complex numbers, and will appear in the form a ± bi.
The graph of this quadratic function shows that there are no real zeros because the graph does not cross the x-axis. Such a graph tells us that the roots of the equation are complex numbers, and will appear in the form a ± bi. |
The complex roots in this example are x = -2 + i and x = -2 - i.
These roots are identical except for the "sign" separating the two terms.
One root is -2 PLUS i and the other root is -2 MINUS i.
Roots that possess this pattern are called complex conjugates (or conjugate pairs).
This pattern of complex conjugates will occur in every pair of complex roots that you will encounter when solving a quadratic equation.
When expressed as factors and multiplied, these complex conjugates will allow for the middle terms containing "i "s to cancel out.
For example: If the roots of the equation are x = -2 ± i, (complex conjugates)
then the factors were ( x - (-2 + i) ) and ( x - (-2 - i) )
Now, multiply these factors:
(x - (-2 + i)) • (x - (-2- i)) = (x + 2 - i)•(x + 2 + i)
= x2 + 2x + xi + 2x + 4 + 2i - xi - 2i - i2 (notice the terms that will cancel)
= x2 + 4x + 4 - (-1) = x2 + 4x + 5
If the middle terms did not cancel, there would be "i "s in the coefficients,
which is not allowed in a quadratic equation.
|
|
 If the roots of a quadratic equation are imaginary (complex),
they always occur in conjugate pairs. |

 The Quadratic Formula Indicates Roots Containing "i ": The Quadratic Formula Indicates Roots Containing "i ":
When a negative value appears under the square root symbol in the quadratic formula, you will know that imaginary/complex roots are going to occur.
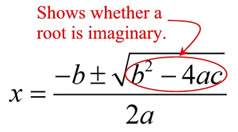
Negative radicand means imaginary (complex) roots. |
Imaginary or complex roots will occur when the value under the radical portion of the quadratic formula is negative.
Notice that the value under the radical portion
is represented by "b2 - 4ac".
So, if b2 - 4ac is a negative value, the quadratic equation
is going to have complex conjugate roots (containing "i "s).
b2 - 4ac is called the discriminant. |
|
 If the discriminant is negative, you have a negative under the radical
and the roots of the quadratic equation will be complex conjugates. |
Read more about the discriminant at "Using the Discriminant".

|
For
calculator help with solve
quadratic
equations 1.
click here. |
|
|
|
For
calculator help
with solve
quadratic
equations 2
click here. |
|
|
|
For calculator help with solve
quadratic
equations
click here. |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|