So, why are we interested in locating the focus of a parabola
and finding conic parabola equations? |
In addition to mathematics, the parabolic curve is present in physics, astronomy, wireless communications, industry, solar energy, engineering, and even optical illusions. Applications of parabolic curves often require specific information about the curve including the focal point. Consider this example which utilizes the focus of a parabola.
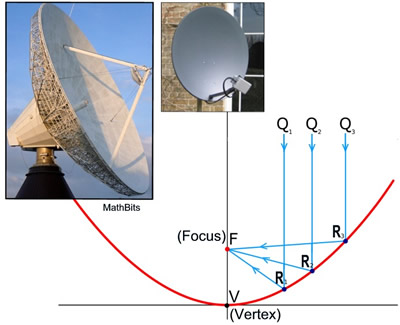 |
A parabolic dish (or parabolic reflector) is a curved surface with a cross-sectional shape of a parabola used to direct light or sound waves. (The 3-D shape is called a paraboloid.)
Any sound waves entering a parabolic dish parallel to the axis of symmetry and hitting the inner surface of the dish are reflected back to the focus.
Radio telescope antennas and satellite dishes use this concept by placing a receiver at the focal point to obtain a concentrated signal.
|
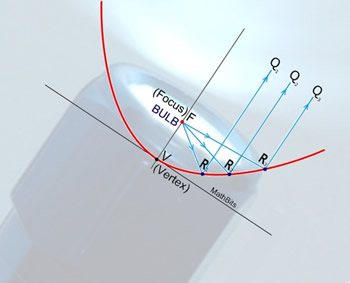
| In a similar manner, the parabolic reflector in a flashlight concentrates the light emitted by the bulb, located at the focal point, into a directed beam of light.
This same principle is at work in your car's headlights and in spotlights.
Where the sound waves were being received by the parabolic dish, the parabolic reflector in a flashlight is directing the light waves outward. |
 |

Other applications of parabolic curves:
|
 |
 |
A well known instance of the parabola in physics is the trajectory of a particle or body in motion under the influence of gravity (without air resistance). Such trajectory is always an approximation of a parabola, and was discovered in the early 17th century by Galileo. Parabolic trajectory can even be used to produce zero-gravity, as seen in the photo with physicist Stephen Hawking. |
 A suspension bridge: a parabola represents the profile of the cable of a suspended-deck suspension bridge.
The curve of the cable created by the chains follows the curve of a parabola.
A suspension bridge: a parabola represents the profile of the cable of a suspended-deck suspension bridge.
The curve of the cable created by the chains follows the curve of a parabola. |
 An arch bridge: a parabola represents the profile of the supporting structure of an arch bridge. This concrete bridge transfers its weight horizontally into abutments.
An arch bridge: a parabola represents the profile of the supporting structure of an arch bridge. This concrete bridge transfers its weight horizontally into abutments. |

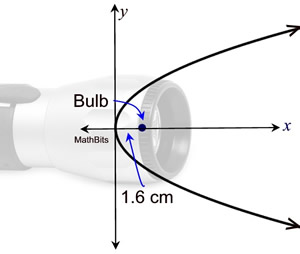
 The parabolic reflector in a flashlight concentrates the light emitted by the bulb, located at the focal point. If the bulb is 1.6 cm from the vertex of the reflector, write an equation for a cross-section of the reflector with its focus on the positive x-axis and its vertex at the origin. The parabolic reflector in a flashlight concentrates the light emitted by the bulb, located at the focal point. If the bulb is 1.6 cm from the vertex of the reflector, write an equation for a cross-section of the reflector with its focus on the positive x-axis and its vertex at the origin.
 |
ANSWER:

|
 The cables of a suspended-deck suspension bridge are in the shape of a parabola. The pillars supporting the cable are 600 feet apart and rise 90 feet above the road. The lowest height of the cable, which is 10 feet above the road, is reached halfway between the pillars. What is the height of the cable from the road at a point 150 feet (horizontally) from the center of the bridge? The cables of a suspended-deck suspension bridge are in the shape of a parabola. The pillars supporting the cable are 600 feet apart and rise 90 feet above the road. The lowest height of the cable, which is 10 feet above the road, is reached halfway between the pillars. What is the height of the cable from the road at a point 150 feet (horizontally) from the center of the bridge?
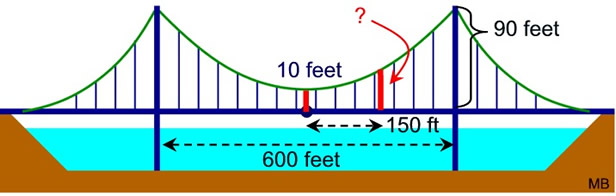
| ANSWER: Let the x-axis be the road and the y-axis be the location halfway between the pillars. The vertex of the parabola will be (0,10). The point on the pillar (300,90) lies on the parabola. We need an equation for the parabola to find (150,y) on the parabola. |
|
|
 A natural stone bridge in Algeria displays an arched parabolic shape. The height of the arch from ground level is 50 feet. The base width at ground level is 30 feet. Using the x-axis as the base, write an equation to model this arch. A natural stone bridge in Algeria displays an arched parabolic shape. The height of the arch from ground level is 50 feet. The base width at ground level is 30 feet. Using the x-axis as the base, write an equation to model this arch.
 |
Position the y-axis so that the vertex (h,k) will be (0,50). The x-intercepts will be (15,0) and (-15,0). Opening down means "p" will appear to be negative.
(x - h)2 = 4p(y - k)
(x - 0)2 = 4p(y - 50)
plug in (15,0) for (x,y):
(15 - 0)2 = 4p(0 - 50)
225 = -200p
p = -9/8
EQUATION:
x2 = 4(-9/8)(y - 50)
x2 = (-9/2)(y - 50) |
 |
|