|
Sets often appear in the investigation of probability.
Venn diagrams may prove useful when displaying a visual of how sets and probabilities are related, especially with overlapping (not mutually exclusive) events.
Let's take a look at examples of how "sets" may be connected to probability.
 |
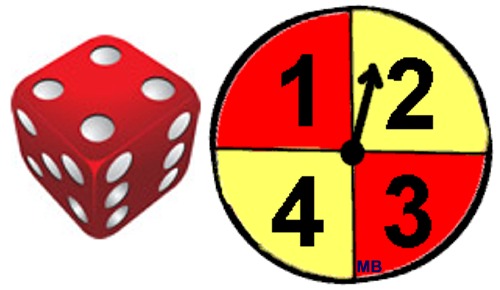 |
| An experiment is setup to first roll a die, followed by spinning a spinner. As shown, the die is a six-sided die and the spinner has four equal divisions labeled 1, 2, 3 and 4. |
• The sample space, S, for this experiment contains 24 possible outcomes.
S = {(1,1), (1,2), (1,3), (1,4),
(2,1), (2,2), (2,3), (2,4),
(3,1), (3,2), (3,3), (3,4),
(4,1), (4,2), (4,3), (4,4),
(5,1), (5,2), (5,3), (5,4),
(6,1), (6,2), (6,3), (6,4)} |
• A possible subset, A, will contain all possibilities of the die rolling an even number and the spinner showing 4.
A = { (2,4), (4.4), (6,4)}
Probability of set A = 3/24 = 1/8
|
• Probability of an outcome belonging to BOTH set A and set B. 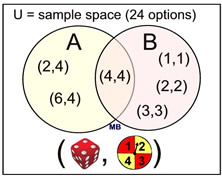 Probability of A ∩ B = 1/24
Probability of A ∩ B = 1/24
|
• A possible subset, B, will contain all possibilities of the die and the spinner showing the same value.
B = {(1,1), (2,2), (3,3), (4,4)}
Probability of set B = 4/24 = 1/6 |

 |
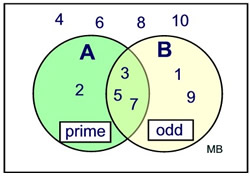 |
Given the Universal set to be integers 1 through 10.
Set A = prime integers.
Set B = odd integers.
The use of a Venn diagram makes it easier to determine the following probabilities. |
Probability of a prime integer
• P(A) = 4/10
|
Probability of prime and odd
• P(A∩B) = 3/10
|
Probability of complement of A
• P(A)C = 6/10
|
Probability of odd integer
• P(B) = 5/10 |
Probability of prime or odd
• P(A∪B) = 6/10 |
Probability of complement of (A∩B)
• P(A∩B)C = 7/10 |

 |
|
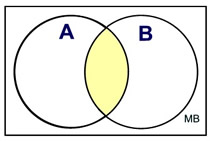
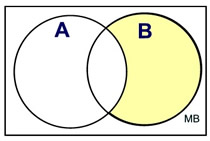
| Given intersecting sets A and B, draw a Venn diagram to depict the following probabilities. |
• P(A or B)
 |
• P(A and B)
 |
• P( AC and B)
 |

 |
|
The Department of Transportation is negotiating a contract regarding roadway improvements. It is estimated that there is a 55% chance that an agreement will be reached on bridge improvements. It is estimated that there is a 65% chance that an agreement will be reached on highway paving improvements. There is a 30% chance that no agreement will be reached on either issue.
a) Find the probability that an agreement will be reached on both issues.
b) Based on your answer, determine whether the agreement on bridge improvements and the agreement on highway paving are independent events. Explain. |
Let B = agreement for bridge improvement
P(B) = 55% = 0.55
Let H = agreement for highway improvement
P(H) = 65% = 0.65
Examine what you know:
• If there is a 30% chance that the decision will NOT be in either set B or set H, then there is an 70% chance that the decision will land in either set B or set H or both.
P (B∪H) = 70% or 0.7
|
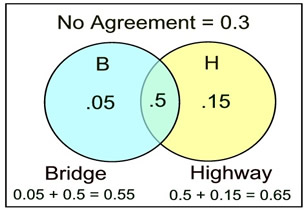 Diagram formed AFTER analysis of the situation.
Diagram formed AFTER analysis of the situation. |
a) An agreement on both issues will fall in the intersection of the two sets:
The formula: P(B∩H) = P(B) + P(I) - P(B∪H)
P(B∩H) = 0.55 + 0.65 - 0.7 = 0.5 (50% chance of agreement on both issues)
b) By definition, if B and H are independent, then P(B∩H) = P(B) • P(H).
P(B∩H) = 0.5
P(B) • P(H) = (0.55) • (0.65) = 0.3575 ≠0.5 (NOT independent) |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|