|
Directions: Read carefully. Choose the best answers.
1. |
Evaluate the following:
a) 5! b) 8P3 c) 0! d) 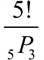 Choose:
Choose:
|
|
|
|
2. |
How many different 5-letter arrangements are there of the letters in the word moose? |
|
|
|
3. |
How many different seven-letter arrangements of the letters in the word HEXAGON can be made if each letter is used only once?
|
|
|
|
4. |
Two cards are drawn at random from a standard deck of cards, without replacement. Find the probability of drawing an 8 and a queen in that order.
|
|
|
|
5. |
Crystal is making personalized invitations for a party. The party-goers are Hallie, Alex, Edward, Alison, Matt, Aleia, Kyle, and Lacey. What is the probability that if Crystal selects a name at random that she will pick a name starting with the letter "A" or the letter "L"?
|
|
|
|
6. |
There are 12 horses in a horse show competition. The top three winning horses receive money. How many possible money winning orders are there for a competition with 12 horses?
|
|
|
|
7. |
Fred is lining up his four golf trophies on a shelf. How many different possible arrangements can he make?
|
|
|
|
8. |
A password consists of three digits, 0 through 9, followed by three letters from an alphabet having 26 letters. If repetition of the digits is allowed, but repetition of the letters is not allowed, determine the number of different passwords that can be made. |
|
|
|
9. |
Six members of a school’s varsity fencing team will
march in a parade. How many different ways can
the players be lined up if Josh, the team captain,
is always at the front of the line?
|
|
|
|
10. |
License plates are formed using four letters followed by a three-digit number without repetition of either letters or digits. Zero may be chosen as the first digit of the number. How many license plates can be formed under this pattern? |
|
|
|
11. |
Determine whether the following situations would require calculating a permutation or a combination:
|
|
|
12. |
A customer selects three different toppings for a pizza. If there are 9 different toppings from which to choose, how many different pizzas can be made?
|
|
|
|
13. |
A teacher chooses a committee of 5 students from the class of 25 students. How many different committees can be chosen?
|
|
|
|
14. |
There are 12 juniors and 20 seniors in the Debate Club. If the members decide to send a team of 2 juniors and 3 seniors to a Debate Conference, how many different conference teams are possible? |
|
|
|
15. |
If 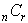 represents the number of combinations of n items taken r at a time,
what is the value of 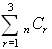 if n = 4 ? |
 |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|