|
|
When determining if events are mutually exclusive,
you are looking for any sharing of elements. |
Two events that have NO outcomes in common
are called mutually exclusive.
These are events that cannot occur at the same time.
When two events, A and B, are mutually exclusive,
the probability of A and B, P(A∩B) = 0.
Remember that "and " implies "intersection" of the sets.
Mutually exclusive sets will not intersect (overlap).
|
 Josh must choose Door A or Door B. He cannot go through both doors at the same time. Mutually exclusive.
Josh must choose Door A or Door B. He cannot go through both doors at the same time. Mutually exclusive. |
For any two mutually exclusive events, the probability that an outcome will
be in one event or the other event is the sum of their individual probabilities.
If A and B are mutually exclusive events,
P(A or B) = P(A) + P(B) |
 |
|
For any two events which are not mutually exclusive, the probability that an outcome
will
be in one event or the other event is the sum of their individual probabilities
minus the probability of the outcome being in both events.
Look out!! Don't get stuck on this one!!!
If events A and B are NOT mutually exclusive,
P(A or B) = P(A) + P(B) - P(A and B) |
|
|


A pair of dice is rolled. What is the probability that the sum of the numbers rolled is either 7 or 11?
Solution:
Six outcomes have a sum of 7:
(1,6), (2,5), (3,4), (4,3), (5,2), (6,1) P(7) = 6/36
Two outcomes have a sum of 11: (5,6), (6,5)
P(11) = 2/36
The sum of the numbers cannot be 7 and 11 at the same time, so these events are mutually exclusive.
P(7 or 11) = P(7) + P(11) = 6/36 + 2/36 = 8/36 = 2/9 |
Sum of Dice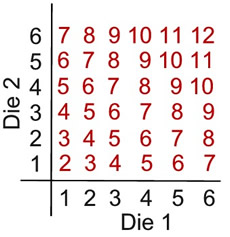 |

A pair of dice is rolled. What is the probability that the sum of the numbers rolled is either an even number or a multiple of 3?
Solution:
Of the 36 possible outcomes, 18 are even sums.
P(even) = 18/36 = 1/2
Sums of 3, 6, 9, and 12 are multiples of 3. There are 12 sums that are multiple of 3.
P(multiple of 3) = 12/36 = 1/3
|
Sum of Dice |
However, some of these outcomes appear in both events. (NOT mutually exclusive)
The sums that are even and a multiple of 3 are 6 and 12.
There are 6 ordered pairs with these sums.
P(even AND a multiple of 3) = 6/36 = 1/6
P(even OR a multiple of 3) = P(even) + P(multiple of 3) - P(even AND multiples of 3)
= 18/36 + 1/3 - 1/6 = 18/36 + 12/36 - 6/36 = 2/3 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|





