We have seen that it is possible to find the probability of compound events, where we have the occurrence of more than one simple event in a sequence. When working with more than one event, you have to be concerned as to whether the first event affects the second event.
|
When determining if events are independent, you are
determining if the events are affecting one another.
|
Two events are said to be independent if the result of the second event is not affected by the result of the first event. The probability of one event does not change the probability of the other event.
If A and B are independent events, the probability of both events occurring is the product of the probabilities of the individual events.
 |
If A and B are independent events,
P(A∩B) = P(A and B) = P(A) • P(B).
(referred to as the "Probability Multiplication Rule")
|
|
Notice the connection between "AND" and "multiplication".
 What is the probability of tossing a head on a penny and then choosing an ace from a standard deck of cards? What is the probability of tossing a head on a penny and then choosing an ace from a standard deck of cards? These are independent events as the second event is not affected by the first.
The probability of BOTH of these events is found by the Multiplication Rule.
The events are independent.
P(head then ace) = P(head) • P(ace) = 1/2 • 4/52 = 2/52 = 1/26. |
 A drawer contains 3 red paper clips, 4 green paper clips, and 5 blue paper clips. One paper clip is taken from the drawer and then replaced. Another paper clip is taken from the drawer. What is the probability that the first paper clip is red and the second paper clip is blue? A drawer contains 3 red paper clips, 4 green paper clips, and 5 blue paper clips. One paper clip is taken from the drawer and then replaced. Another paper clip is taken from the drawer. What is the probability that the first paper clip is red and the second paper clip is blue? Because the first paper clip is replaced, the sample space of 12 paper clips
does not change from the first event to the second event. The events are independent.
P(red then blue) = P(red) • P(blue) = 3/12 • 5/12 = 15/144 = 5/48. |
When you toss a coin, the probability of getting a head is 1 out of 2 or ½.
 |
If you toss the coin again, the probability of getting a head is still 1 out of 2 or ½.
If you toss a coin 10 times and get a head each time, you may think that your luck of
tossing a tail is increasing since it has not yet appeared. This is not the case.
These events are independent events and do not affect one another.
The probability of tossing a tail is 1 out of 2 or ½ regardless of how many heads were tossed previously. |

If the result of one event IS affected by the result of another event,
the events are said to be dependent.
If A and B are dependent events, the probability of both events occurring
is the product of the probability of the first event and the probability of the second event
once the first event has occurred.
|
If A and B are dependent events, and A occurs first,
P(A and B) = P(A) • P(B, once A has occurred)
... and is written as ...
P(A∩B) = P(A and B) = P(A) • P(B | A)
|
|
The notation P(B | A) is called a "conditional probability"
and is read "the probability of event B given that event A has occurred".
 A bag contains 3 green marbles and 2 red marbles. A marble is drawn, not replaced, and then a second marble is drawn. What is the probability of drawing a green marble followed by drawing a red marble? A bag contains 3 green marbles and 2 red marbles. A marble is drawn, not replaced, and then a second marble is drawn. What is the probability of drawing a green marble followed by drawing a red marble? By not replacing the marble after the first draw, the probability of the second draw is affected.
The sample space of the second draw has changed, leaving only 4 marbles.
The events are dependent.
P(green then red) = P(green) • P(red given green occurred) = 3/5 • 2/4 = 6/20 = 3/10. |
 A drawer contains 3 red paper clips, 4 green paper clips, and 5 blue paper clips. One paper clip is taken from the drawer and is NOT replaced. Another paper clip is taken from the drawer. What is the probability that the first paper clip is red and the second paper clip is blue? A drawer contains 3 red paper clips, 4 green paper clips, and 5 blue paper clips. One paper clip is taken from the drawer and is NOT replaced. Another paper clip is taken from the drawer. What is the probability that the first paper clip is red and the second paper clip is blue? Because the first paper clip is NOT replaced, the sample space of the second event is changed. The sample space of the first event is 12 paper clips, but the sample space of the second event is now 11 paper clips.
The events are dependent.
P(red then blue) = P(red) • P(blue) = 3/12 • 5/11 = 15/132 = 5/44. |

Sampling with, and without, replacement: |
When working with the probability of two (or more) events occurring, it is important to determine if finding the probability of one of the events has an effect on any of the other events.
Consider the following example:
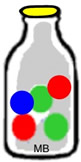
What is the probability of drawing a red marble,
then drawing a blue marble from this jar?
The probability of drawing a red marble = 2/5.
The probability of drawing a blue marble = 1/5.
BUT...
|
|
• The 1/5 probability of drawing a blue marble assumes all 5 marbles are in the jar.
•
What happens if you draw the first marble and do NOT put that marble back in the jar before drawing the second marble? If the marble is not "replaced", the probability of the second drawing changes, since there are less marbles in the jar.
The probability of drawing a red marble = 2/5.
 The probability of drawing a blue marble is now = 1/4. The probability of drawing a blue marble is now = 1/4.
Let's compare the two different answers:
| With Replacement: |
Without Replacement: |
 |
The probability of drawing a red marble = 2/5.
Put the marble back in the jar.
The probability of drawing a blue marble = 1/5. (of the 5 in the jar)
Answer: 2/5 • 1/5 = 2/25 |
|
 |
The probability of drawing a red marble = 2/5.
Do not put marble back in jar.
The probability of drawing a blue marble = 1/4. (of the 4 left in jar)
Answer: 2/5 • 1/4 = 2/20 = 1/10 |
|
|
|
In relation to probability, the word "replacement" most often refers to situations where something can be "removed" (drawn, chosen, etc.) from the sample set, and then replaced (or not replaced).
•
"With replacement":
Choosing a ball, a card, a marble, or other object, and then replacing the item back into the sample space each time an event occurs.
Example: Choosing a card from a deck and then putting the card back into the deck before drawing another card.
• "Without replacement": Choosing a ball, a card, a marble, or other object, and then NOT replacing the item back into the sample space before choosing another object.
Example: Choosing a card from a deck and not replacing it to the deck before drawing another card.
The sample space for the second card draw has now been changed to one less card.
 Be on the lookout for the word "replacement" as a clue.
Be on the lookout for the word "replacement" as a clue.
| With Replacement: the events are independent. Probabilities do NOT affect one another. |
| Without Replacement: the events are dependent. Probabilities DO affect one another. |




