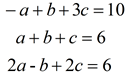|
Directions: Questions for Parts II, III, and IV are long response questions. You will need paper, pencil and a graphing calculator to work out the problems. Check your answer after solving each problem by clicking the ANSWER button. |
25. The scoring results of an Intelligence Test are normally distributed. The mean is 92 and the standard deviation is 9.3. What percent, to the nearest tenth of a percent, of students taking the test scored between 84 and 101?
|
|
|
26. Graph the function f (x) = x3 - 4x2 + x + 6 and write f (x) as a product of linear factors.
|
|
|
27. The Ice Cream Shoppe conducts a survey to determine the popularity of its three new dipping flavors (raspberry, peppermint and mango) for soft ice cream cones. Of 150 customers surveyed, 90 liked raspberry, 65 liked peppermint, 45 liked mango, 20 liked both raspberry and peppermint (but not mango), 5 liked both peppermint and mango (but not raspberry), 15 liked both raspberry and mango (but not peppermint), 15 liked all three, and 20 did not like any flavors. What is the probability that a customer liked mango, given that he/she liked raspberry?
|
|
|
28. Given h(x) = (x2 + 9)(x - 5), find the two imaginary roots associated with this function.
|
|
|
29. 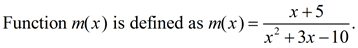 a) State the domain of function m(x).
a) State the domain of function m(x).
b) Find any asymptotes associated with m(x).
|
|
|
30. Express 8i5 - 2i4 + 8i3 + 3i2 + 11i in simplest form. |
|
|
31. Prove that a3 + b3 = (a + b)(a2 - ab + b2) is an identity. |
|
|
32. Given the equation 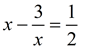 , find the solution(s). , find the solution(s). |
|
|
33. Find all solutions, real or imaginary: x4 - 81 = 0
|
|
|
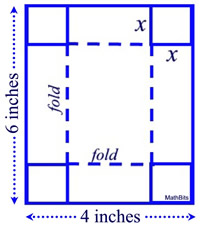
34. A small box is to be formed by cutting and folding a 4 inch by 6 inch rectangular sheet of cardboard. Congruent squares with sides of x inches are cut from each corner of the cardboard as shown.
a) Create a function, V (x), that can be used to find the volume of the box.
b) When graphed, determine the restricted domain of function V (x).
c) Determine to the nearest hundredth of a cubic inch, the maximum volume possible under these conditions.
|
 |
|
35. Solve algebraically for a, b and c: 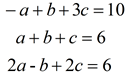 |
|
|
36. Following a law suit when a woman was burned by spilling hot coffee, McDonalds now serves coffee at 155º F. The room temperature at McDonalds is 70º F. According to Newton's Law of Cooling, the rate of change of the temperature of hot coffee is proportional to the difference between the temperature of the coffee and the surrounding room temperature. In this situation, we have the model
|
| |
T(t) = the temperature of the coffee after t minutes
t = the time in minutes
Ta= the room temperature (ambient temperature) |
a) According to this model, what is the temperature of the coffee when it is initially poured from the coffee pot at t = 0 ?
b) How long, in minutes (to the nearest tenth of a minute), will it take for the coffee to cool to the serving temperature of 155º F. ?
|
|
37. A tsunami is a series of ocean waves that send surges up to 100 feet high onto land. They are caused by underwater earthquakes or explosions. The water level in a tsunami will initially fall below its normal level, then rise an equivalent distance above the normal level, finally returning back to its normal level. Assume the period of this cycle to be 18 minutes.
A tsunami is observed from a coastal pier where the normal depth of the water is 10 feet. Following the cycle pattern described above, the tsunami has an amplitude of 10 feet above the normal water depth.
The depth of the water will vary sinusoidally with time.
a) Graph one full cycle of the wave, with time in minutes on the x-axis and water height in feet on the y-axis.
b) Write a sine function of the form f (x) = A sin(Bx) + D to model this tsunami.
c) Predict the depth of the water 12 minutes after the tsunami first reaches the pier to the nearest tenth of a foot.
d) What will be the minimum depth of the water during this cycle, and when will it occur?
e) Interpret what will be seen by observers when the cycle reaches its minimum depth.
|
|
|
|
|
|
|

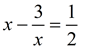 , find the solution(s).
, find the solution(s).