|
Directions: Questions for Parts II, III, and IV are long response questions. You will need paper, pencil and a graphing calculator to work out the problems. Check your answer after solving each problem by clicking the ANSWER button. |
25. 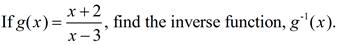
|
|
|
26. On what interval(s) is the function f (x) = (x2 - 9)(x2 - 1) decreasing?
Round to nearest thousandths, if needed.
|
|
|
27. Given 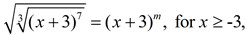 find the value of the constant m. find the value of the constant m.
|
|
|
28. Given f (x) = x4 + 3x3 - 2x2 - 5x - 1 and g(x) = | 1.2x | - 6, find the solutions to f (x) = g(x). Round to nearest hundredths, if needed.
|
|
|
29. A nursery states that Higan cherry trees can be grown in both temperature Zones 4 and 5 across the United States. The life spans of 25 New York state Higan cherry trees grown in Zone 4 and 25 New York state Higan cherry trees grown in Zone 5 were compared. The mean life spans of the trees were:
Life Span Zone 4 |
Life Span
Zone 5 |
Mean = 11.6 years |
Mean = 21.8 years |
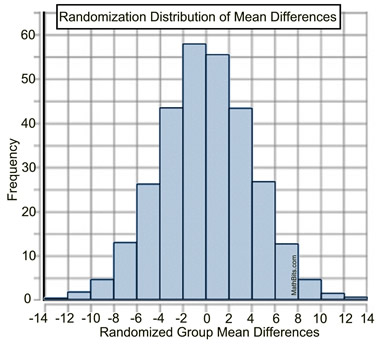
A computer simulation of a Randomization Test is shown at the right with 300 re-samples being considered.
a) Determine the mean difference in the life spans using "Zone 5 - Zone 4", and explain its meaning in the context of this problem.
b) Based upon the information given, determine if the observed mean difference in life spans was of statistical significance. Explain.
|
|
|
30. Given (a + b)(a2 +2ab + b2) = 27, find the value of a + b. |
|
|
31. Solve the equation: 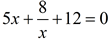 . Express answer in simplest a + bi form. |
|
|
| 32. Polonium-210 is a radioactive element with the property that every 138 days the mass of the element in a sample is reduced by half. (It's half-life is 138 days.) |
|
a) If A0 represents the original mass of polonium-210, write a function to model the amount of polonium-210 remaining at a designated time, t, in days.
b) If you have 100 micrograms of polonium-210, how much will remain after 60 days? |
|
33. Solve for x: 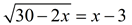 Justify your solution(s). Justify your solution(s).
|
|
|
34. The U.S. Forest Service states that there is a correlation between a tree's breadth and its age. Formulas using the circumference of trees exist to determine the ages of various types of trees. A park ranger wants to develop a formula for determining the ages of red oak trees in his forest. He measures the circumferences of red oak trees whose ages he knows, and calculates their diameters to the nearest tenth. His results are shown in the table at the right.
a) Find a linear regression equation the ranger can use to model this data. Round to the nearest thousandths.
b) Determine the correlation coefficient.
c) What does the correlation coefficient for this data tell you about the data?
d) If a tree is 30 years old, what will be the diameter of the tree, to the nearest tenth, according to this model?
|
Diameter (in) |
Age
(yrs) |
2.6 |
15 |
5.0 |
20 |
6.3 |
25 |
7.0 |
28 |
10.2 |
40 |
12.5 |
50 |
15.2 |
60 |
|
|
35. a) Prove that (a - b)3 = a3 - 3a2b + 3ab2 - b3 is an identity.
b) Use this identity to expand and simplify (3x - 5)3.
|
|
|
36. Rodrigo, Caroline, and Kevin are in charge of bringing snacks for a tailgate party prior to the big game. The table below shows the items they purchased separately at the same local store.
|
|
SNACKS |
2-litre bottles of Coca-Cola |
15.75 oz Bags Lay's Potato Chips |
16 oz. Bags of Gold's Pretzel Sticks |
Dollar Amount Spent |
Rodrigo |
4 |
4 |
2 |
25.48 |
Caroline |
2 |
4 |
3 |
25.58 |
Kevin |
3 |
2 |
4 |
23.12 |
Calculate the individual price of each snack purchased for the tailgate party by algebraically solving a 3x3 system. |
|
37. A polynomial function is given as P(x) = x3 - 3x2 + 4.
a) Factor completely, the expression x3 - 3x2 + 4.
b) Graph P(x).
c) Find the coordinates of all relative (local) maxima. Round to nearest tenths if needed.
d) Describe the end behavior of P(x).
e)The graphs of equations of degree 3 often cross the x-axis in three locations, representative of the the three roots. Explain what is happening with this function as it relates to crossing the x-axis. |
|
|
|
|
|
|
|

