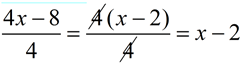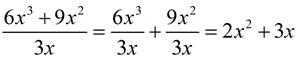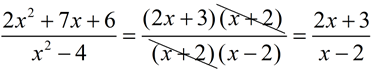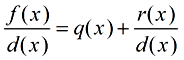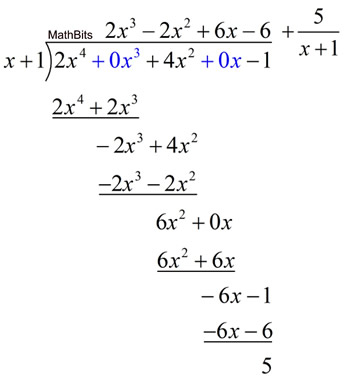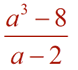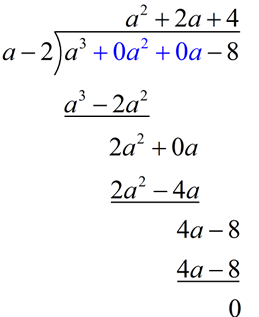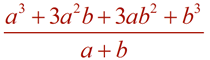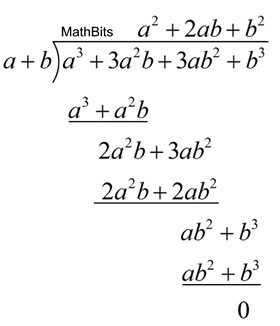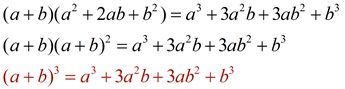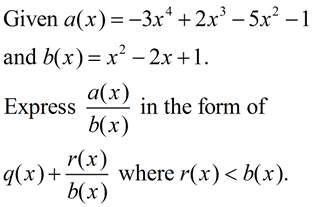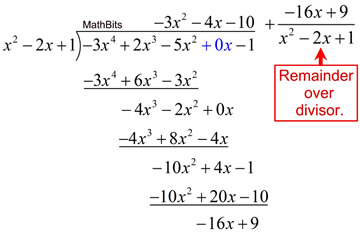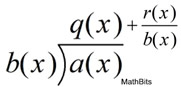We have seen simple division of polynomials in Algebra 1, such as:
Division with factoring the numerator and reducing: 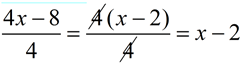 |
Division with creating separate fractions and reducing:
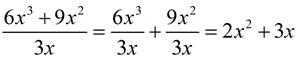 |
Dividing a factorable polynomial by a binomial:
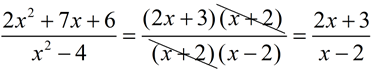
|
It is now time to expand our division skills to allow us to conquer more situations.
 Long Division Long Division |
|
|
Our first "new" strategy is LONG DIVISION. Yes, it is the same idea that you learned in elementary school. Let's see how our new process resembles what you already know how to do.
Numerical Long Division Process:
 |
Algebraic Long Division Process:
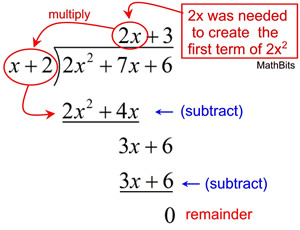 There is no remainder to
There is no remainder to
be listed in this problem.
|
Division Algorithm:
More formally stated, the division algorithm algebraically states that:
if f (x) and d (x)≠0 are polynomials such that the degree of d (x) ≤ the degree of f (x),
then there exists unique polynomials q (x) and r (x) such that
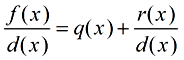
and the degree of r (x) < the degree of d (x).
If r (x) = 0, then d (x) divides evenly into f (x), making d (x) a factor of f (x).
|
This algorithm is simply saying that when the two polynomials are divided (
f (
x) ÷
d (
x)), the solution will be the quotient,
q(
x), plus a remainder expressed as the remainder over the divisor,
r(
x)/
d(
x).

Let's examine algebraic long division in a variety of situations. We will be assuming that the divisors in these examples are not zero (i.e., in Example 1, assume x - 3 ≠0).
|
Divide: (2x3 + 4x2 + 5x - 1) by (x - 3) |
Process:
1. Start the division by asking, "What term multiplied times x will give 2x3 ? "
In this problem, the answer is 2x2. |
|
2. Multiply your answer to this question times the divisor (x - 3), lining up the similar terms. Then subtract (being careful to change the signs). |
3. Bring down the next available term in the dividend.
|
4. Repeat this process (from step 1 through step 3) until all terms from the dividend have been used. |
5. If there is a remainder, place the remainder over the divisor and add it to your quotient answer. (This is the same manner of expressing the remainder that you saw in elementary long division.) |

|
Divide: (3x2 + x3 - 2x + 6) by (x - 1) |
Be sure that the polynomial is in descending order (by powers).
|
(x3 + 3x2 - 2x + 6) by (x - 1) |
If not, re-write the polynomial into descending order before beginning the division.
|
|
|

|
Divide: (2x4 + 4x2 - 1) by (x + 1) |
Look for any missing terms in the descending order. |
2x4 + 0x3 + 4x2 + 0x - 1 |
Replace missing terms with a coefficient of 0 to "hold" their location in the division process. |
|
|

|
Divide: 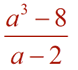
|
Remember to replace missing terms with 0 coefficients to "hold" their positions in the division. |
|
Did you notice that this division problem is an example of factoring the difference of perfect cubes?
Remember the formula:
a3 - b3 = (a - b)(a2 + ab + b2)
In this problem, a3 = a3 and b3 = 8 (making b = 2).
a3 - 8 = (a - 2)(a2 + 2a + 4) |

|
(x6 + 2x5 +5x3 +4x 2 + 6) ÷ (x3 + 2) |
Be sure to line-up the similar terms before subtracting when the divisor contains a power greater than 1. |
|
When preparing to subtract, be sure that your terms are lined-up under similar terms. |
Notice in this problem that we replaced the missing terms with zero coefficients to "hold" their places in the division, but in effect, these missing terms were never utilized in this problem. |
|
|
Multiple variables: |
|
Follow the same process when working with multiple variables. |
Since a2 + 2ab + b2 = (a + b)2, the division in this problem has shown that:
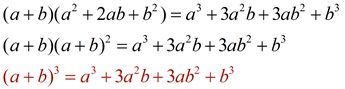 This is the pattern we saw under Factoring and Perfect Cubes (section "Cubing Binomials").
This is the pattern we saw under Factoring and Perfect Cubes (section "Cubing Binomials").
We will be seeing this "pattern" for the expansion of ( a + b) 3 again.
|
|
Problem with Different wording:
|
QUESTION:
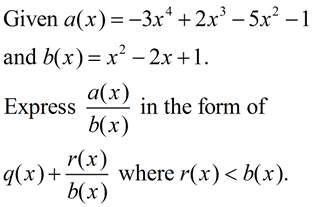 |
SOLUTION:
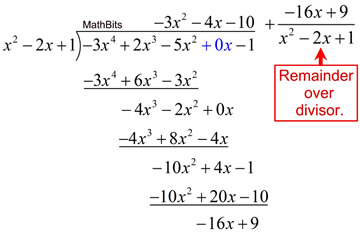 |
This question is asking you to divide the two given polynomials and to express the answer as a quotient plus a remainder divided by the divisor. In other words, it is simply asking you to divide these polys as we have been doing. |
|
|