|
Directions: Read carefully. Choose the best answers.
1. |
Which of the following functions is even?
|
|
|
Choose:
|
|
2. |
Regarding the graph at the right, the parabola is:
|
|
|
| |
|
3. |
Is the parent absolute value function,
f (x) = | x |, odd, even, or neither?
|
|
|
Choose:
|
|
4. |
If f (x) = x3 + x, which of the following statements must be true?
(Check all that apply, and hit SUBMIT!) |
|
|
5. |
Given the functions shown below, determine which of the functions are odd, even or neither. Show your algebraic work to confirm your answers.
| 1) f (x) = 4x3 - 9 |
2) f (x) = x2 + 4x + 4 |
| 3) f (x) = x5 + 4x3 - 2x |
4) f (x) = | x | + 2 |
5) 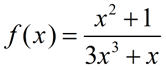 |
6) 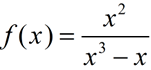 |
|
| |
|
6.
|
Which of the following functions is odd?
Choose:
|
|
|
7. |
The graph shown at the right is a portion of an even function on the interval [-4,4].
Complete the graph on the given interval.
|
|
|
|
8. |
Sketch the graph of an odd function that has the following properties. There is more than one correct answer.
Domain is [-5,5]
Range is [-2,2]
Increasing on the interval (-3,3)
Decreasing on intervals (-5,-3) and (3,5)
|
 |
|
|
9. |
The graph shown at the right is a portion of a function on the interval [-4,4].
a) Complete the graph on the given interval assuming the graph to be even.
b) Complete the graph on the given interval assuming the graph to be odd. |
|
|
|
10. |
Show that the product of two even functions is an even function.
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|