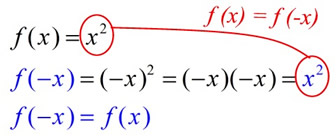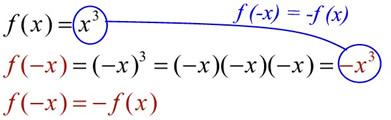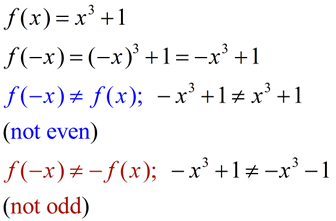|
Odd and even functions are special types of functions with special characteristics.
|
The trick to working with odd and even functions is to remember to plug in (-x) in place of x and see what happens.
Examine f (-x).
If there is no change = even. If there is a negation = odd.
|
 A function is "even" when f (-x) = f (x) for all x. A function is "even" when f (-x) = f (x) for all x.
When you plug in -x, you get back the same function with which you started.
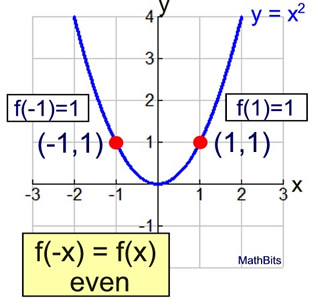
Even functions are symmetric about the y-axis. [(x,y) → (-x,y)]
This graph remains unchanged when reflected across the y-axis.
Example:
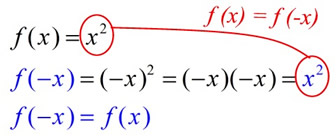
This function is even.
When you plug in (-x), you get the original function back. Nothing changes.
|
 |
Functions containing even exponents (powers) may be even functions.
For example, functions such as f (x) = x2,
f (x) = x4, f (x) = x6, ... are even functions.
But, functions such as f (x) = (x - 1)2 are NOT even functions.
f (x) = (x - 1)2 = x2 - 2x + 1 BUT f (-x) = (-x - 1)2 = x2 + 2x + 1
f (x) ≠
f (-x) → not even
 |
Do not make the generalization that if a function has an even power that the function must be even. |

 A function is "odd" when f (-x) = - f (x) for all x. A function is "odd" when f (-x) = - f (x) for all x.
When you plug in -x, you get back the negation of the function with which you started.
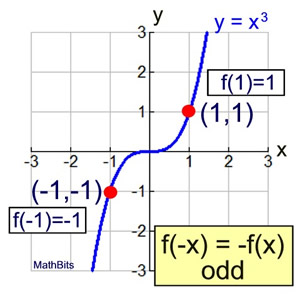
Odd functions are symmetric about the origin. [(x,y) → (-x,-y)]
The graph remains unchanged after a rotation of 180 degrees about the origin.
Example:
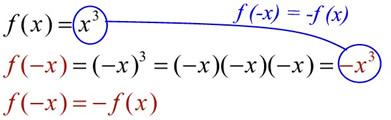
This function is odd.
When you plug in (-x), you get the negation
of the original function back.
|
 |
Functions containing odd exponents (powers) may be odd functions.
For example, functions such as f (x) = x3, f (x) = x5, f (x) = x7, ... are odd functions.
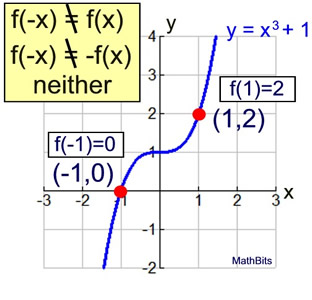
But, functions such as f (x) = x3 + 2 are NOT odd functions.
f (x) = x3+ 2 BUT f (-x) = (-x)3 + 2 = -x3 + 2
The negation of f (x) is -x3 - 2, which is not the same as -x3 + 2.
f (-x) ≠ -f (-x) → not odd
 |
Do not make the generalization that if a function has an odd power that the function must be odd. |

Neither Odd nor Even Functions |
 While odd and even functions are interesting functions, the majority of functions do not fall into either of these categories. All of these "other" functions are referred to as "neither", when being compared to the odd and even function definitions. While odd and even functions are interesting functions, the majority of functions do not fall into either of these categories. All of these "other" functions are referred to as "neither", when being compared to the odd and even function definitions.
Example:
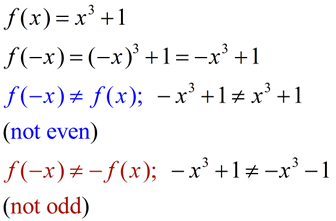
This function is neither.
|
 |

Properties of Odd and Even Functions |
• The only function that is both odd and even is f (x) = 0.
• If a function is odd, the absolute value of that function is even.
Regarding algebra of functions (+, - , •, /):
• The sum of two even functions is even.
• The sum of two odd functions is odd.
• The difference of two even functions is even.
• The difference of two odd functions is odd.
• The product of two even functions is even.
• The product of two odd functions is even.
• The quotient of two even functions is even.
• The quotient of two odd functions is even.
Regarding composition of functions ((f o g)(x)):
• The composition of two even functions is even.
• The composition of two odd functions is odd.
• The composition of an even function and an odd function is even.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|