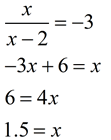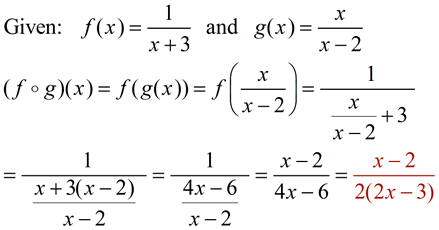At times, finding the domain of a composite function can be confusing and difficult to understand. There may be hidden obstacles that prevent certain values from completing their trips through a composition, thus eliminating theses values as possible domain elements. The composition of certain rational functions, for example, may present internal "obstacles" for certain domain values. Let's examine what happens to values as they "travel" through a composition of rational functions. Consider the following example:
Visual Interpretation of this example:
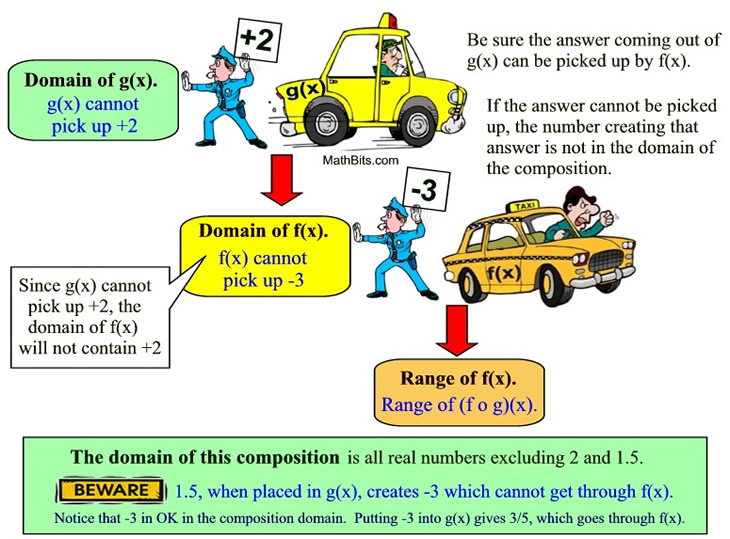
The domain of a composition will be those values which can "move through" to the end of the composition. The "obstacle" is whether all of the values created by g(x), in this case, can be "picked up" by function f (x). Algebraic Interpretation of this example: 1. Function g(x) cannot pick up the value +2 since it creates a zero denominator. Consequently, the composition also cannot pick up the value of +2. 2. The answers coming out of function g(x) come out in the form 3. When does
4. The domain of
When you determine the domain of a composition, you must of course consider any restrictions on the starting function. If a value cannot get through the starting function, it cannot get through the composition. But what about additional restrictions? If you find the composition of the two functions algebraically, you can examine your algebraic answer to determine any additional restrictions on the domain of the composition.
Final solution: The domain of the composition is all real numbers with the exclusion of 2 and 1.5.
Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
|||||||||||||||||||

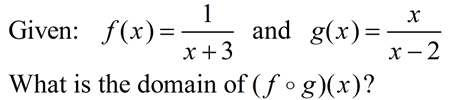
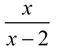 .
. 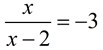 since these values create an answer that cannot progress through the composition
since these values create an answer that cannot progress through the composition