|
Functions can be transformed (distorted) in various ways to help them better represent processes and behaviors found in the real world. You have already seen references to the concept of transformations in algebra and in geometry. The various types of functional transformations shown on this page will be a review, and enhancement, of those concepts.
Transformations are used to move, resize and distort graphs of functions.
We will be examining the following changes to f (x):
- f (x), f (-x), f (x) + k, f (x + k), kf (x), f (kx)
reflections translations dilations
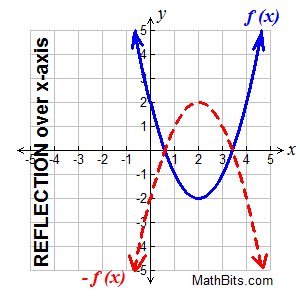
Reflections of Functions: -f (x) and f (-x) |
 Vertical reflection:
reflection over the x-axis. Vertical reflection:
reflection over the x-axis.
-f (x) reflects f (x) over the x-axis
|
|
Reflections are mirror images.
Think of "folding" the graph over the x-axis.
On a grid, you used the formula
(x,y) → (x,-y) for a reflection in the
x-axis, where the y-values were negated.
In functional notation
we can write
(x, f (x)) → (x, -f (x)).
|
 |
|
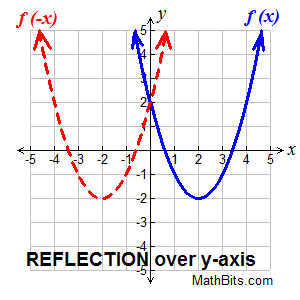
 Horizontal reflection:
reflection over the y-axis.
f (-x) reflects f (x) over the y-axis Horizontal reflection:
reflection over the y-axis.
f (-x) reflects f (x) over the y-axis |
|
Reflections are mirror images.
Think of "folding" the graph over the y-axis.
On a grid, you used the formula (x,y) → (-x,y) for a reflection in the y-axis, where the x-values were negated.
In function notation we can write
(x, f (x)) → (-x, f (-x)).
|
Translations of Functions: f (x) + k and f (x + k) |
 Vertical shift: Vertical shift:
vertical translation (straight up or straight down)
f (x) + k moves f (x) up or down
|
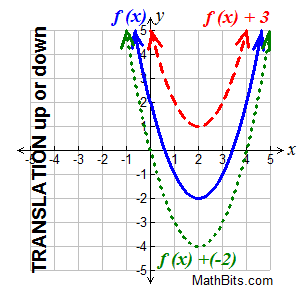
Changes occurs "outside" the function (affecting the y-values). |
This translation is a "slide" straight up or down.
• if k > 0, the graph moves upward k units.
• if k < 0, the graph moves downward k units.
Remember the formula (x,y) → (x,y + k) moving a figure upward or downward on a graph.
In function notation, we can write
(x, f (x)) → (x, f (x) + k).
You are adding the value
of k to the y-values of the function.
|
|
|
 Horizontal shift: Horizontal shift:
horizontal translation (left or right)
f (x + k) moves f (x) left or right |
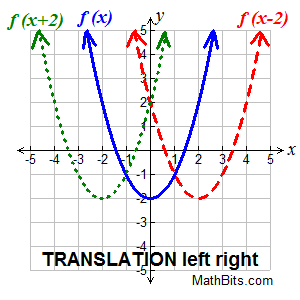
Changes occurs "inside" the function (affecting the x-values). |
This translation is a "slide" left or right.
• if k > 0, the graph moves to the left k units.
• if k < 0, the graph moves to the right k units.
 This can be very confusing!
k positive moves graph left
k negative moves graph right.
Consider this scenario: This can be very confusing!
k positive moves graph left
k negative moves graph right.
Consider this scenario: Suppose lunch = 11 am. If this changes to (lunch+2) = 11 am, then lunch is 9 am. Adding 2 made it happen sooner (which graphically means move to the left).
|
Hint: To remember which way to move the graph, set (x + k) = 0. The solution will tell you in which direction to move and by how much.
f (x - 2): x - 2 = 0 gives x = +2, move right 2 units.
f (x + 3): x + 3 = 0 gives x = -3, move left 3 units. |
|
|
Up to this point, we have only changed the "position" of the graph of the function.
Now, we will start changing "distorting" the shape of the graphs.
| Dilations of Functions: kf (x) and f (kx) |
 Vertical Stretch or Compression Vertical Stretch or Compression
k f (x) stretches/shrinks f (x) vertically |
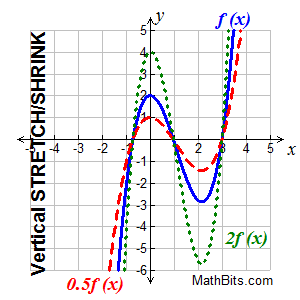
"Multiply y-coordinates"
(x, y) becomes (x, ky)
"vertical dilation"
|
A vertical stretch pulls graph away from the x-axis.
A vertical compression (or shrink) squeezes graph toward the x-axis.
• if k > 1, the graph is vertically stretched by multiplying each of its y-coordinates by k.
• if 0 < k < 1 (a fraction), the graph vertically compressed (or shrunk) by multiplying each of its y-coordinates by k.
• if k should be negative, the vertical stretch or shrink is followed by a reflection across the x-axis.
|
|
|
| Notice that the "roots" on the graph above stay in their same positions on the x-axis. The graph gets "taffy pulled" up and down from the locking root positions. The y-values change. |
 Horizontal Stretch or Compression Horizontal Stretch or Compression
f (kx) stretches/shrinks f (x) horizontally |
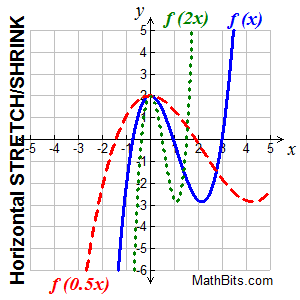
"Divide x-coordinates"
(x, y) becomes (x/k, y)
"horizontal dilation"
|
A horizontal stretching pulls the graph away from y-axis
A horizontal compression (or shrink) squeezes the graph toward the y-axis.
• if k > 1, the graph is horizontally shrunk (or compressed) by dividing each of x-coordinate by k.
• if 0 < k < 1 (a fraction), the graph is horizontally stretched by dividing each of its x-coordinates by k.
• if k should be negative, the horizontal stretch or shrink is followed by a reflection in the y-axis. |
|
|
| Notice that the "roots" on the graph above have now moved, but the y-intercept stays in its same initial position for all graphs. The graph gets "taffy pulled" left and right from the locking y-intercept. The x-values change. |
Transformations of Function Graphs |
|
reflect f (x) over the x-axis
|
f (-x) |
reflect f (x) over the y-axis |
f (x) + k |
shift f (x) up k units |
f (x) - k |
shift f (x) down k units |
f (x + k) |
shift f (x) left k units |
f (x - k) |
shift f (x) right k units |
k•f (x) |
multiply y-values by k (k > 1 stretch, 0 < k < 1 shrink vertical) |
f (kx) |
divide x-values by k (k > 1 shrink, 0 < k < 1 stretch horizontal) |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|