Practice Page
Directions: Read carefully. You should be able to solve these questions without your graphing calculator. Choose the best answers.

1.
Given: f (x) = (2x + 1)(x + 3)(x - 2)
For what values of x is f (x) > 0 ?
(Check all that apply, and hit SUBMIT!)		 fbigger0

x < -3

-3 < x < -½

-3 < x < 2

-½ < x < 2

x > -½

x > 2

      

 

 

2.
Regarding the graph at the right, the function is:
polygraph2

Choose:
 
odd.
 
increasing on interval (-∞,-3).
 
positive on interval (3,∞).
 
symmetric about the origin.
 

 

 

3.
Given: f (x) = (2x + 1)(x + 3)(x - 2)
How many relative maxima does this function have?
sheeplook
  

Choose:
 
one
two
three
none

 

 

4.
A fifth degree polynomial function is shown below.
Which of the statements are NOT true about this function?
(Check all that apply, and hit SUBMIT!)

leading coefficient is positive

function is odd

only two relative maximums

only two intervals of decreasing

positive from x = -2 to x = 1.75

exactly 5 zeroes

as x → ∞, y → ∞

      

polygraph1a

 

 

5.
Given h(x) = -(x - 1)(x + 2)(x - 5)
What are the end behaviors of the graph of this function?

Choose:
 
beh1
beh2
 
 
beh3
 
beh4
 

 

 

6.
Which of the following polynomial functions could be represented by the graph at the right?

Choose:
 
f (x) = x3 + 4x2 + x - 1
 
f (x) = x3 + 3x2 + x + 1
 
f (x) = x3 + 4x2 + x + 1
 
f (x) = x3 + 3x2 + x - 1
matchgrapha

 

 

7.
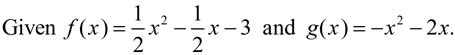
ffnew
Which of the statements are true about these functions?
(Check all that apply, and hit SUBMIT!)

the graph of g(x) opens downward

function g(x) is even

in f (x), as x → ∞, y → ∞

f (x) and g(x) share a zero

f (x) is negative on interval (-2,3)

g(x) is positive on interval (-2,0)

in g(x), as x → -∞, y → ∞

      

functiondoor

 

 

8.
Which of the following functions represents a polynomial function with degree 3, roots x = 0, x = -1 and x = 2, and with end behavior approaching positive infinity as x approaches negative infinity?

Choose:
 
g (x) = x(x + 1)(x - 2)
g (x) = x(x - 1)(x + 2)
 
g (x) = -x(x + 1)(x - 2)
g (x) = -x(x - 1)(x + 2)

 

 

9.
Given: f (x) = (x + 1)2(3 - x)
Which of the following statements is FALSE regarding its graph?

Choose:
 
As x → ∞, f (x) → -∞.
 
There is one relative maximum point.
 
There is one relative minimum point.
 
As x → -∞, f (x) → -∞.
falsesheep

 

 

10.
Given: f (x) = x2 - 16
On which interval(s) is this function positive?

Choose:
 
(- ∞, 0)
 
(0, ∞)
 
(-16, ∞)
 
(-∞, -4) and (4, ∞)
positive

 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".