|
Directions: Read carefully. Choose the best answers.
1. |
Given f (x) =(x + 2)(x - 1)(x - 3), find:
|
|
| a) Find the y-intercept of f (x).
Choose:
|
b) Find the zeros of f (x).
|
| c) On which given interval is f (x) increasing?
Choose:
|
d) On which given interval does
f (x) have a relative maximum?
Choose:
|
|
|
2. |
Which choice describes the end behavior for the graph shown at the right?
Choose:
|
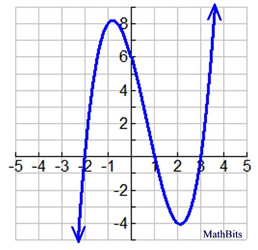 |
|
3. |
A function is defined by the equation f (x) = 5x + 2. If the domain is 2 ≤ x ≤ 6, find the minimum value in the range of the function.
|
|
|
|
4. |
Find the domain of the function:
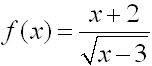 |
|
|
|
5. |
Which graph possesses the following features?
• decreasing on (2,3)
• increasing on (3,∞)
• relative minimum at (3,-4)
• positive on (-1,2)
|
|
|
|
6. |
If the domain of f (x) = 2x + 1 is {-2 < x < 3}, which integer is not in the range?
|
|
|
|
7. |
Given the graph shown at the right.
|
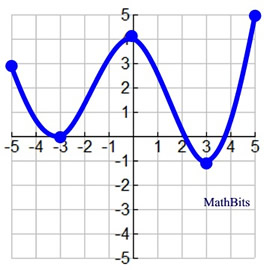 The domain of this function is [-5,5]. |
a) Which coordinate(s) represents relative maxima for this graph?
Choose:
b) Which interval(s) represents the function increasing?
Choose:
|
c) What is the range of this function?
Choose:
d) What is the absolute maximum value of this function?
Choose:
|
e) What is the absolute minimum value of this function?
Choose:
|
8. |
If the domain of g(x) = (x - 1)2 + 4 is limited to {-3,-2,-1,0,1,2,3,4}, what is the maximum value of the range? |
|
|
|
9. |
Which of the choices best represents the intervals upon which the function shown at the right is considered "positive"?
Choose:
|
 The domain of this function is [-5,5]. The domain of this function is [-5,5]. |
|
10. |
Which of the following functions has the characteristics:
• domain all Reals
• increasing (-∞,
∞)
•
positive (0, ∞)
• as x → ∞, y → ∞
• as
x → -∞, y → 0 |
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|