When two or more transformations are combined to form a new transformation, the result is called a sequence of transformations, or a composition of transformations. Remember, that in a composition, one transformation produces an image upon which the other transformation is then performed.
Sequences of transformations applied to functions work in a similar manner.

When working with composition of transformations, it was seen that the
order in which the transformations were applied often changed the outcome. This same potential problem is present when working with a sequence of transformations on functions.
For example, given the function of
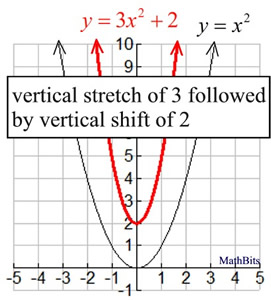
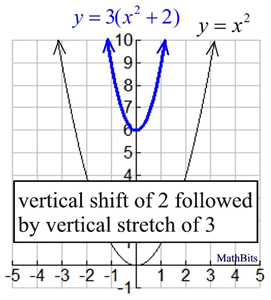
y = x2, a
vertical stretch of 3 followed by a
vertical shift of 2 will not produce the same graph as a
vertical shift of 2 followed by a
vertical stretch of 3.
There are, however, certain situations where the order is not important and the same graph will exist regardless of the order in which the transformations are applied.
Be careful not to assume that this will be the case in all problems.
To determine when order of sequences of transformations affects function graphs:
|
• If two or more of the transformations have a vertical effect on the graph, the order of those transformations will most likely affect the graph.
•
If two or more of the transformations have a horizontal effect on the graph, the order of those transformations will most likely affect the graph.
• Vertically oriented transformations and horizontally oriented transformations to not affect one another. |
|

Consider the problem f (x) = 2(x + 3) - 1.
The parent function is f (x) = x, a straight line.
It can be seen that the parentheses of the function have been replaced by x + 3,
as in f (x + 3) = x + 3. This is a horizontal shift of three units to the left from the parent function.
The multiplication of 2 indicates a vertical stretch of 2, which will cause to line to rise twice as fast as the parent function. The parent has a slope of 1, whereas this new function will have a slope of 2.
The subtraction of 1 indicated a vertical shift of one unit down. |
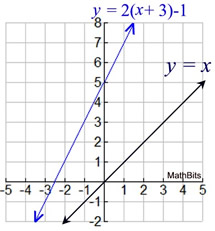 |
| There was a pattern to the order in which this problem was analyzed (horizontal shift - - vertical stretch - - vertical shift). This pattern is similar to order of operations. The parentheses were done first, then any multiplication/division, followed by any addition/subtraction. |
 Remember that a horizontal shift is associated with a change in the x-coordinate value (expressed as a linear expression -- x with a power of 1). Expressions such as (x + 3) and (x - 4) can represent a horizontal shift, but expressions such as (x2 + 3) and (x3 - 4) cannot. Remember that a horizontal shift is associated with a change in the x-coordinate value (expressed as a linear expression -- x with a power of 1). Expressions such as (x + 3) and (x - 4) can represent a horizontal shift, but expressions such as (x2 + 3) and (x3 - 4) cannot. |
It is often necessary to perform trasnformations in a
certain order to guarantee the arrival at the correct graph. The following steps will help to ensure a correct solution.
Steps for a Sequence of Transformations
Apply the following steps when graphing by hand a function containing more than one transformation. Apply the transformations in this order:
| |
1. Start with parentheses (look for possible horizontal shift)
(This could be a vertical shift if the power of x is not 1.)
2. Deal with multiplication (stretch or compression)
3. Deal with negation (reflection)
4. Deal with addition/subtraction (vertical shift) |
These steps are basically just following order of operations.
(parenthesis, mult/divide, negation, add/subtract)
|
It is possible to express transformations,
in a form similar to:
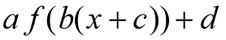 remembering that x needs a power of one for a horizontal shift.
remembering that x needs a power of one for a horizontal shift. |
where
a = vertical stretch or compression
b = horizontal stretch or compression
c = horizontal shift when x power is 1
d = vertical shift |
|


Graph by hand:
f (
x) = (
x - 3)
2 + 2
Parent function: y = x2
Step 1: Do the inner most parentheses first.
y = (x - 3)2 has a horizontal shift which shifts
the graph 3 units to the right. Notice the power
on x is 1.
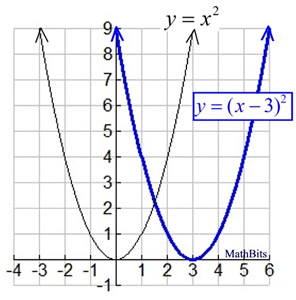
|
Step 2: Now apply the vertical shift of +2
to the new graph from Step 1.
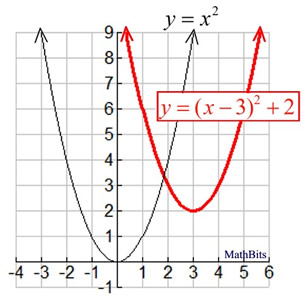
|


Describe the transformations associated with
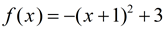 .
.
The parent function is y = x2.
Following the steps:
1. there is a horizontal shift of 1 units to the left
(the power of x is 1 connecting it to the x-coordinate).
2. there is no stretch of compression
3. there is a reflection in the x-axis.
4. there is a vertical shift of 3 upward |
 |

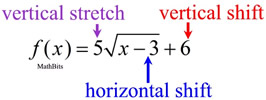
 a) Describe the transformations associated with
a) Describe the transformations associated with 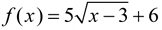 .
.
The parent function is 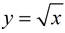 .
.
Following the steps:
1. there is a horizontal shift of 3 units to the right
(the power of x is 1 connecting it to the x-coordinate).
2. there is a vertical stretch of 5
3. there is no reflection
4. there is a vertical shift of 6 upward
b) When drawing the graph of this function by hand, does it matter in which order these transformations are applied?
Yes. By examining the "types" of transformations, we can observe that two vertical oriented transformations are being applied, which tells us that we need to be careful that the transformations are applied in the proper order, if we want to end up with the correct graph.


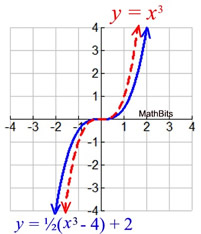
Describe the transformations associated with
f (
x) = ½ (
x3 - 4) + 2.
 Do you see the pitfall with this problem?
Do you see the pitfall with this problem?
At first glance, you may want to say that there is a horizontal shift 4 units right.
WRONG!!!
The (
x3 - 4) does not indicate a horizontal shift. Yes, it is parentheses, but it is
not x to the first power, which would associate the 4 with the
x-coordinate. This is a
vertical shift, not a horizontal shift.
The parent function is y = x3.
Following the steps:
1. there is a NO horizontal shift.
There is a vertical shift of 4 units downward indicated in the
parentheses.
2. there is a vertical compression of ½.
3. there is no reflection
4. there is a vertical shift of 2 upward
There is no apparent vertical shift in the graph because the vertical shifts cancel each other out. y = ½ x3 - 2 + 2 = ½ x3 |
 |
In the problem shown above, the form af (b(x + c) + d for examining transformations can still apply for ordering, but you must be aware that the parentheses, in this case, is not a horizontal shift since the power of x is not 1. |


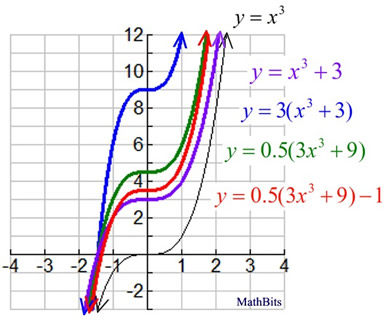
Graph by hand:
f (
x) = 0.5(3
x3 + 9) - 1
Parent function: y = x3
Using the formula
a f (
b(
x + c)) +
d for separations, we get
f (
x) = 0.5(
3(
x3 + 3)) - 1
But again, the inner most parentheses in this problem does not indicate a horizontal shift since the power of
x is not 1. This inner most parentheses is indicating a vertical shift.
Follow the order of operations to prepare the graph.
Step 1: (in purple)
Do the inner most parentheses first,
y = x3 + 3 which shifts the graph 3 units up.
Step 2: (in blue)
Apply a vertical stretch of 3.
y = 3(x3 + 3) which multiplies y-values times 3.
Step 3: (in green)
Apply a vertical stretch of 0.5.
y = 0.5(3(x3 + 3)) which multiplies y-values times ½.
Step 4: (in red)
Apply the vertical shift of -1,
y = 0.5(3(x3 + 3)) -1 which shifts graph 1 unit down.
Final graph in red. |
|