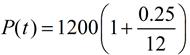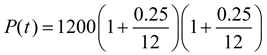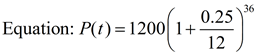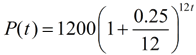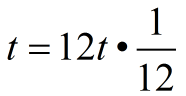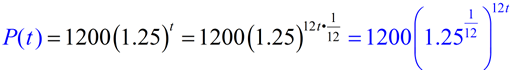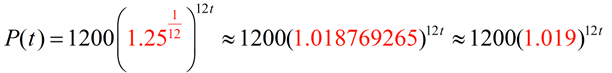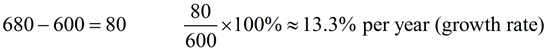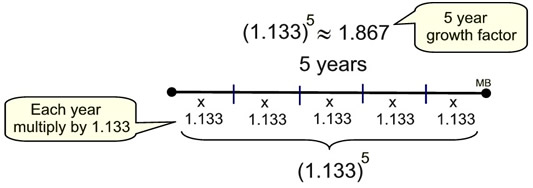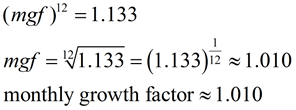When working with exponential equations, you may run into a question that wants the resulting equation (or a given equation) re-stated in relation to a different time reference, such as "in months" instead of "in years". Such questions do not want you to change the conditions of the problem. Instead, these questions simply want an equivalent form of the existing equation.
 Let's start with an example and see how to approach the solution:
Let's start with an example and see how to approach the solution:
EXAMPLE: A study of the annual population of spiders in a certain area shows that the population, P(t), can be modeled by the equation P(t) = 1200(1.25)t, where t represents the number of years since the study began. Write an equation to approximate the population in terms of the monthly rate of growth. |
Remember the formulas: Increasing: y = a (1 + r)x Decreasing: y = a(1 - r)x
(1 ± r is the growth factor, while r is the growth rate)
From the information given, we can see that there were 1200 spiders when the study began.
The given formula tells us that the population of spiders is increasing
at a yearly rate of 25%.
So each year we have all of the previous spiders plus 25% more of those spiders (100% + 25% more).
1 + r = 1.00 + 0.25 = 1.25.
Let's start our solution by examining the annual formula, P(t) = 1200(1.25)t = 1200(1 + 0.25)t :
Year 1: P(t) = 1200(1.25)1
P(t) = 1200(1.25)
|
Year 2: P(t) = 1200(1.25)2
P(t) = 1200(1.25)(1.25) |
Year 3: P(t) = 1200(1.25)3
P(t) = 1200(1.25)(1.25)(1.25) |
We see from these first three years, that the growth rate is being "compounded "
(the percentage, 1.25, is always multiplied by the previous year's population of spiders).
The compounding is done yearly. Keep this in mind!
So, what happens if we simply divide the yearly rate of growth (0.25)
by 12 to create a monthly rate of growth?
Month 1:
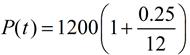 |
Month 2:
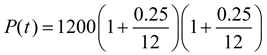 |
By doing this, we are now compounding the growth monthly.
The question is, will compounding monthly give us the same answer as compounding annually?
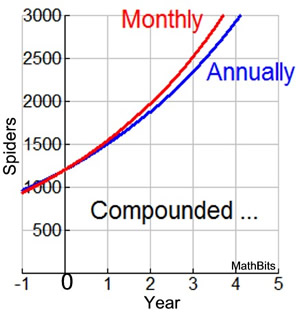
Let's look at a graph and the computations of our situation after three years.
Compounded Annually (Yearly) |
Compounded Monthly |
Equation: P(t) = 1200(1.25)3
After 3 years = 2343.75 spiders.
P(t) = 1200(1.25)t |
3 years = 36 months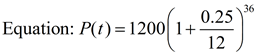 After 3 years =
2520.899787 spiders.
After 3 years =
2520.899787 spiders.
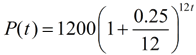 |
|
The graph shows that compounding the population growth monthly will not yield the same results as compounding the growth annually. (The results from compounding monthly are increasing more rapidly over time.)

Comparing the rates of growth (or decay) will only yield the same results when both rates are converted to the same compounding period.
In this example, the compounding period is "annually". So we cannot convert the problem to compounding "monthly" and expect to get approximately the same result. |
|
So, how do we get the equation needed for this question?
First, we need to avoid changing the conditions of this problem.
We do not want to set the problem up to compound monthly.
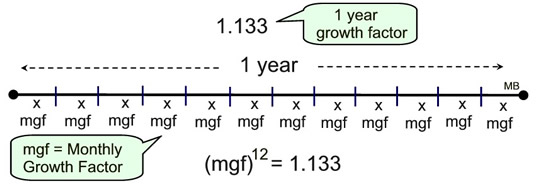
We simply want to write an equivalent form of the same equation that will allow for the time period to be calculated in months. If we want to express the "time" in months, we need 12t in the formula, instead of t.
For example, for one year, t = 1, we want 12 months (12t = 12(1) = 12).
How can we write the formula with t replaced by 12t,
yet keep the same equation?
We will put our skills with exponents to work.
Remember: 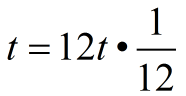
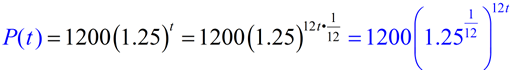
Notice how we used the rules of working with exponents to place the 1/12 inside the parentheses.
Remember, that raising a power to a power, multiplies the two powers.
If we simplify the interior of the parentheses, we will have the new monthly rate of growth equation:
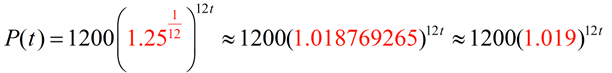
Where the yearly rate of growth for this population of spiders was 25%,
the monthly rate of growth is approximately 1.9%.
Remember 1.019 = 1 + 0.019 and 0.019 = 1.9%.
ANSWER:
Monthly Rate of Growth Equation:
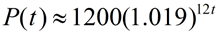
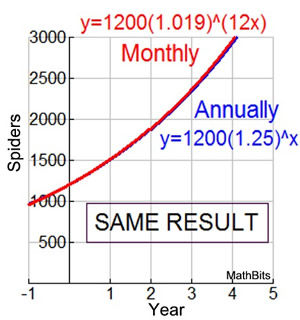
As the graph at the right shows, this new monthly based equation yields approximately the same results as the original annual equation.
Note: There may be slight discrepancies between the graphs as the years increase due to the rounding of the value in the interior of the parentheses. (It is for this reason that the question is asking for an equation to approximate the population in terms of the monthly rate of growth.)
|
 |